(四)解决办法只要将相同未知量前的系数化为绝对值相等的值即可利用加减法进行消元．——青夏教育精英家教网—

(四)解决办法只要将相同未知量前的系数化为绝对值相等的值即可利用加减法进行消元．【查看更多】

作文 (15分)
假定你是某外国语学校的学习委员，经常看到有同学抄袭作业，针对这种现象，你将在下周的班会上组织全班同学讨论这一现象，并以“My opinion on copying others homework”为主题作中心发言，请事先用英语写一篇发言稿。
注意：
1．发言稿须包括以下内容要点；
A．抄袭的主要原因。
B．抄袭的危害及解决办法。
C．简要表明自己的态度。
2．词数：不少于120个词；
3．发言稿的开头已给出，不计入总词数。
May I have your attention, please? My topic today is about copying others’ homework.
As we know, some students copy others’ homework. ______________________

查看答案和解析>>

作文 (15分)
假定你是某外国语学校的学习委员，经常看到有同学抄袭作业，针对这种现象，你将在下周的班会上组织全班同学讨论这一现象，并以“My opinion on copying others homework”为主题作中心发言，请事先用英语写一篇发言稿。
注意：
1．发言稿须包括以下内容要点；
A．抄袭的主要原因。
B．抄袭的危害及解决办法。
C．简要表明自己的态度。
2．词数：不少于120个词；
3．发言稿的开头已给出，不计入总词数。
May I have your attention, please? My topic today is about copying others’ homework.
As we know, some students copy others’ homework. ______________________

查看答案和解析>>

如图，正方形ABCD的两条对角线把正方形ABCD分割成四个全等的等腰直角三角形，将它们分别沿正方形ABCD的边翻折，可得到一个面积是原正方形ABCD面积2倍的新正方形EFGH．
请你在图1，图2，图3中完成：将矩形分割成四个三角形，然后将其沿矩形的边翻折，分别得到面积是原矩形面积2倍的三个新的四边形：菱形、矩形、一般的平行四边形．

查看答案和解析>>

24、先阅读下面的材料，然后解答问题：
已知：如图1等腰直角三角形ABC中，∠B=90°，AD是角平分线，交BC边于点D．
求证：AC=AB+BD．
证明：如图1，在AC上截取AE=AB，连接DE，则由已知条件易知：Rt△ADB≌Rt△ADE（AAS）
∴∠AED=∠B=90°，DE=DB
又∵∠C=45°，∴△DEC是等腰直角三角形．
∴DE=EC．
∴AC=AE+EC=AB+BD．
我们将这种证明一条线段等于另两线段和的方法称为“截长法”．
解决问题：现将原题中的“AD是内角平分线，交BC边于点D”换成“AD是外角平分线，交BC边的延长线于点D，如图2”，其他条件不变，请你猜想线段AC、AB、BD之间的数量关系，并证明你的猜想．

查看答案和解析>>

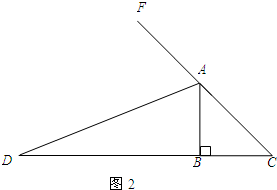
如图1，小明将一张矩形纸片沿对角线剪开，得到两张三角形纸片（如图2），量得他们的斜边长为10cm，较小锐角为30°，再将这两张三角纸片摆成如图3的形状，但点B、C、F、D在同一条直线上，且点C与点F重合.（在图3至图6中统一用F表示）

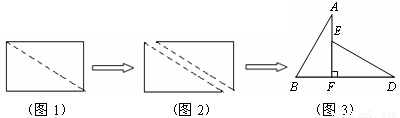
小明在对这两张三角形纸片进行如下操作时遇到了三个问题，请你帮助解决.

（1）将图3中的△ABF沿BD向右平移到图4的位置，使点B与点F 重合，请你求出平移的距离；

（2）将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置，A₁F交DE于点G，请你求出线段FG的长度；

（3）将图3中的△ABF沿直线AF翻折到图6的位置，AB₁交DE于点H，请说明：AH=DH.

查看答案和解析>>

练习册

高中

初中

小学