
题目列表(包括答案和解析)
小明同学学习了几何中的对称后,忽然想起了过去做过的一道题:有一组数排列成方阵如图所示,试计算这组数的和.小明想:方阵就像正方形,正方形既是轴对称图形,又是中心对称图形,能不能利用轴对称和中心对称的思想来解决方阵的计算问题呢?
小明试了试,竟然得到了非常巧妙的方法,你也能试试看吗?
从方阵上的数可以看出,一条对角线上的数都是5,若把这条对角线当做对称轴,把正方形翻折一下,对称位置的两数之和都是10(如图),这样方阵中数的和为(4+3+2+1)×10+5×5=125.于是原方阵中数的和为125.

也可以考虑,把方阵绕中心旋转180°,就得到另一方阵,再加到原来的方阵上去,就得到所有数是10的方阵(如图),这一方阵数的和为10×5×5=250.于是原方阵中数的和为![]() =125.
=125.

从前有个国王,他有三个儿子.大王子只喜欢读书,二王子只知道习武,小王子的兴趣十分广泛,爱读书,爱习武,还爱玩.
有一天,国王对王子们说:“你们的祖父母去世早,你们可能都记不得他们的年龄了,谁能告诉我,你们的祖父母都活了多大岁数?”
二王子问:“可以问您几个问题吗?”
国王回答:“只能问一个.”
“啊,问一个问题就猜到祖父母的年龄,太困难了,这恐怕连神仙也难办到!”大王子自言自语地说.
国王又问小王子说:“你行吗?”小王子点了点头.大王子和二王子都很惊讶.
小王子说:“请您把祖父的年龄放在前面、祖母的年龄放在后面,组成一个四位数,然后将这个四位数平方,接着减去祖母年龄的平方,然后除以祖父年龄的100倍,最后减去祖母的年龄,把所得的数告诉我.”
国王不知道小王子想干什么,心算了一阵说:“得3129”.
小王子马上答道:“祖父活到31岁,祖母活到29岁.”国王高兴地站起来说:“对极啦,就是这两个年龄!”“为什么让父王算一道题,就能把祖父母的年龄算出来呢?”“只许问一个问题,要猜出两人的年龄,还不能直接去问,你是怎样算的呢?”两位哥哥不停地问着小王子.
小王子的妙算是让父王算出一个四位数,使得千位和百位上的数字与祖父的年龄有关;十位和个位上的数字与祖母的年龄有关.
小王子的算法是:祖父的年龄放在前面、祖母的年龄放在后面组成的四位数是3129,将这个四位数平方,得9790641;减去祖母年龄的平方,得9789800;除以祖父年龄的100倍,得3158;最后减去祖母的年龄,得(31292-292)÷(31×100)-29=3129.
大王子问:“为什么这样一定可以得到3129呢?”
小王子解释,可以利用整式的乘除的知识,把上面的算式以另一种方式做一下变形:
[(31×100+29)2-292]÷3100-29=(312×1002+2×31×100×29+292-292)÷3100-29=(312×1002+2×31×100×29)÷3100-29=31×100+2×29-29=3129.
原来小王子像魔术师变魔术一样,在计算中加了一点“伪装”,这就是“将四位数平方,减去祖母年龄的平方,除以祖父年龄的100倍,减去祖母的年龄”.其实这些步骤与计算祖父、祖母的年龄毫无关系,目的是使这种计算更隐蔽、更神秘(其实,我们只需根据由祖父、祖母年龄组成的四位数就可以知道祖父、祖母的年龄).
同学们,你能通过整式的有关知识对小王子的算法作出解释吗?
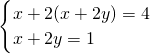

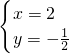
 (2)
(2)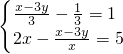 .
.
|
| 1 |
| 2 |
|
|
|
|
| 1 |
| 2 |
|
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com