
题目列表(包括答案和解析)
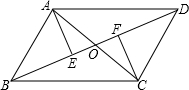 如图,?ABCD中对角线AC、BD相交于点O,AE⊥BD于E,CF⊥BD于F.
如图,?ABCD中对角线AC、BD相交于点O,AE⊥BD于E,CF⊥BD于F.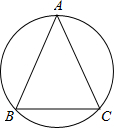 (2012•宜昌模拟)如图,△ABC内接于⊙O,AC=AB,∠BAC=50°,
(2012•宜昌模拟)如图,△ABC内接于⊙O,AC=AB,∠BAC=50°,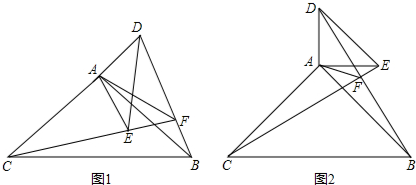
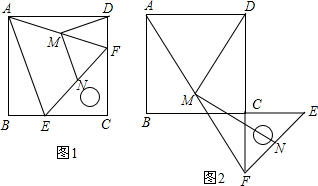 (2013•山西模拟)操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(2013•山西模拟)操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN. (2012•朝阳)如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.
(2012•朝阳)如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com