已知二次函数y=ax²+bx+c，且ac＜0，则它的图象经过(　　 )

　(A)一、二、三象限 　　　　(B)二、三、四象限

　(C)一、三、四象限 　　　　(D)一、二、三、四象限

（本题9分）体育课上，老师训练学生的项目是投篮，假设一名同学投篮后，篮球运行的轨迹是一段抛物线，将所得轨迹形成的抛物线放在如图所示的坐标系中，得到解析式为y＝－x²＋x＋3.3（单位：m）．请你根据所得的解析式，回答下列问题：

  　(1)球在空中运行的最大高度为多少米？

 　 (2)如果一名学生跳投时，球出手离地面的高度为2.25m，，请问他距篮球筐中心的水平距离是多少？

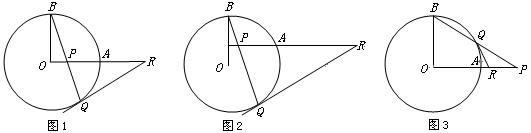
有这样一道习题：已知：如图1，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点(不与O、A重合)，BP的延长线交⊙O于Q，R是OA的延长线上一点，且RP=RQ.说明：RQ为⊙O的切线. （无须证明）

　　请探究下列变化：

　　变化一：交换题设与结论.

如图1，已知OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点(不与O、A重合)，BP的延长线交⊙O于Q，过Q点作⊙O的切线交OA的延长线于R.说明：RP=RQ.（要证明）

　　变化二：运动探求.

　　(1)如图2，若OA向上平移，变化一中的结论还成立吗？(只需交待判断) 答：_________.

　　(2)如图3，如果P在OA的延长线上时，BP交⊙O于Q，过点Q作⊙O的切线交OA的延长线于R，变化一中的结论还成立吗？为什么？

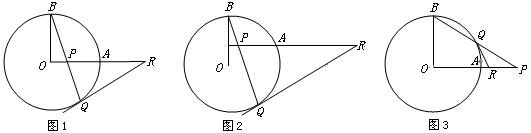
（本题满分12分）有这样一道习题：已知：如图1，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点(不与O、A重合)，BP的延长线交⊙O于Q，R是OA的延长线上一点，且RP=RQ.说明：RQ为⊙O的切线. （无须证明）

　　请探究下列变化：

　　变化一：交换题设与结论.

如图1，已知OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点(不与O、A重合)，BP的延长线交⊙O于Q，过Q点作⊙O的切线交OA的延长线于R.说明：RP=RQ.（要证明）

　　变化二：运动探求.

　　(1)如图2，若OA向上平移，变化一中的结论还成立吗？(只需交待判断) 答：_________.

　　(2)如图3，如果P在OA的延长线上时，BP交⊙O于Q，过点Q作⊙O的切线交OA的延长线于R，变化一中的结论还成立吗？为什么？ 来]

下面是按一定规律排列的一列数：

　　　 第1个数：；

　　　 第2个数：；

　　　 第3个数：；

　　　 ……

　　　 第个数：．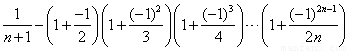

　　　 那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）

　　A．第10个数 　　　B．第11个数 　　　C．第12个数　　　 D．第13个数

　　3．已知：a为有理数，a3+a2+a+1=0，求1+a+a2+a3+…+a2012的值．

　　4．已知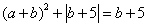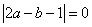：，，求ab的值。

　　5．当整数k为何值时，方程9x-3=kx+14有正整数解？并求出正整数解