
题目列表(包括答案和解析)
| • |
| 3 |
| • |
| 2 |
| • |
| 3 |
| • |
| 2 |
| • |
| 3 |
| • |
| 2 |
| 32 |
| 99 |
| • |
| 3 |
| • |
| 2 |
| 32 |
| 99 |
| • |
| 3 |
| • |
| 8 |
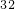 可化成0.323232….如果我们要把0.
可化成0.323232….如果我们要把0.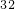 化成分数,可以用以下方法进行:设x=0.
化成分数,可以用以下方法进行:设x=0.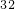 ,即x=0.323232…,两边同乘以100,得100x=32.323232…,即100x=32+0.323232…,所以100x=32+x.解这个方程得:x=
,即x=0.323232…,两边同乘以100,得100x=32.323232…,即100x=32+0.323232…,所以100x=32+x.解这个方程得:x=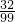 ,即0.
,即0.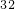 =
=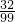 .试用上面的方法把0.
.试用上面的方法把0.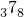 化成分数.
化成分数.| x2-2x-4 |
| x-1 |
| (x2-x)+(-x+1)+(-5) |
| x-1 |
| 5 |
| x-1 |
| 3 |
| 1+x2 |
| 3 |
| 1+x2 |
| 3 |
| 1+x2 |
| 4x2+8x+7 | ||
|
| 4x2+8x+7 | ||
|
| 2 |
| (x+1)2+1 |
| 1 | 2 |
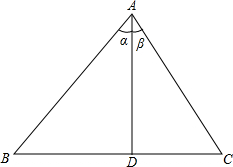 sin30°,根据如图,设计一种方案,解决问题:
sin30°,根据如图,设计一种方案,解决问题: ,同时也知道,sin(30°+30°)=sin60°≠sin30°+sin30°,根据如图,设计一种方案,解决问题:
,同时也知道,sin(30°+30°)=sin60°≠sin30°+sin30°,根据如图,设计一种方案,解决问题: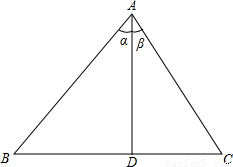
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com