某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：

　　●操作发现：

      在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是         （填序号即可）

     ①AF=AG=AB；②MD=ME；③整个图形是轴对称图形；④∠DAB=∠DMB．

●数学思考：

  在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD和ME具有怎样的数量和位置关系？请给出证明过程；

●类比探索：

  在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状．

  答：           ．

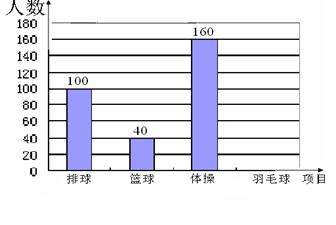
学校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛球、体操课．学生可根据自己的爱好任选其中一项，老师根据学生报名情况进行了统计，并绘制了右边尚未完成的扇形统计图和频数分布直方图，请你结合图中的信息，解答下列问题：

（1）该校学生报名总人数有多少人？　　

（2）从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分

之几？　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

（3）将两个统计图补充完整．　　　　　　　　　　　　　　　　　　　　　

学校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛球、体操课．学生可根据自己的爱好任选其中一项，老师根据学生报名情况进行了统计，并绘制了右边尚未完成的扇形统计图和频数分布直方图，请你结合图中的信息，解答下列问题：
（1）该校学生报名总人数有多少人？　　
（2）从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分
之几？　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
（3）将两个统计图补充完整．　　　　　　　　　　　　　　　　　　　　　
      

某数学兴趣小组开展了一次活动，过程如下：

设∠BAC=θ（0°＜θ＜90°）．现把小棒依次摆放在两射线之间，并使小棒两端分别落在射线AB，AC上．

活动一：

如图甲所示，从点A₁开始，依次向右摆放小棒，使小棒与小棒在端点处互相垂直，A₁A₂为第1根小棒．

数学思考：

（1）小棒能无限摆下去吗？答：　_________　．（填“能”或“不能”）

（2）设AA₁=A₁A₂=A₂A₃=1．

①θ=　_________　度；

②若记小棒A_2n﹣1A_2n的长度为a_n（n为正整数，如A₁A₂=a₁，A₃A₄=a₂，…）求出此时a₂，a₃的值，并直接写出a_n（用含n的式子表示）．

活动二：

如图乙所示，从点A₁开始，用等长的小棒依次向右摆放，其中A₁A₂为第1根小棒，且A₁A₂₌AA₁．

数学思考：

（3）若已经摆放了3根小棒，θ₁=　_________　，θ₂=　_________　，θ₃=　_________　；（用含θ的式子表示）

（4）若只能摆放4根小棒，求θ的范围．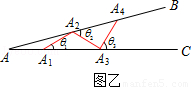

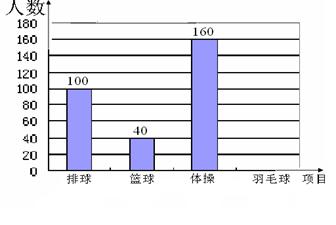
学校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛球、体操课．学生可根据自己的爱好任选其中一项，老师根据学生报名情况进行了统计，并绘制了右边尚未完成的扇形统计图和频数分布直方图，请你结合图中的信息，解答下列问题：

（1）该校学生报名总人数有多少人？　　

（2）从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分

之几？　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

（3）将两个统计图补充完整．