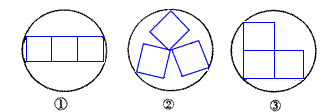
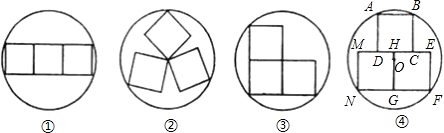
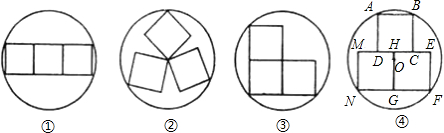
在一节数学实践活动课上,吕老师手拿着三个正方形硬纸板和几个不同的圆形的盘子,他向同学们提出了这样一个问题:已知手中圆盘的直径为13cm,手中的三个正方形硬纸板的边长均为5cm,若将三个正方形纸板不重叠地放在桌面上,能否用这个圆盘将其盖住?问题提出后,同学们七嘴八舌,经过讨论,大家得出了一致性的结论是:本题实际上是求在不同情况下将三个正方形硬纸板无重叠地适当放置,圆盘能盖住时的最小直径.然后将各种情形下的直径值与13cm进行比较,若小于或等于13cm就能盖住,反之,则不能盖住.吕老师把同学们探索性画出的四类图形画在黑板上,如下图所示.
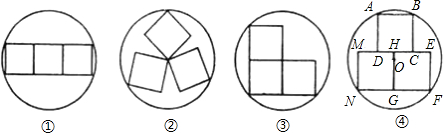
(1)通过计算,在①中圆盘刚好能盖住正方形纸板的最小直径应为
cm.(填准确数)
(2)图②能盖住三个正方形硬纸板所需的圆盘最小直径为
cm图③能盖住三个正方形硬纸板所需的圆盘最小直径为
cm?(结果填准确数)
(3)按④中的放置,考虑到图形的轴对称性,当圆心O落在GH边上时,此时圆盘的直径最小.请你写出该种情况下求圆盘最小直径的过程.(计算中可能用到的数据,为了计算方便,本问在计算过程中,根据实际情况最后的结果可对个别数据取整数)
(4)由(1)(2)(3)的计算可知:A.该圆盘能盖住三个正方形硬纸板,B.该圆盘不能盖住三个正方形硬纸板.你的结论是
.(填序号)