练习册

  • 练习册
  • 试题
    证明:连接OQ. 能力提高 【查看更多】

     

    题目列表(包括答案和解析)

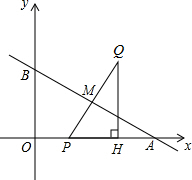    如图直线y=-
    12
    x+2    分别交x轴、y轴于点A和B，点P（t，0）是x轴上一动点，P、Q两点关于直线AB轴对称，PQ交AB于点M，作QH⊥x轴于点H．
    （1）求tan∠OAB的值；
    （2）当QH=2时，求P的坐标；
    （3）连接OQ，是否存在t的值，使△OQH与△APM相似？若存在，求出t的值；若不存在，说明理由．

    查看答案和解析>>

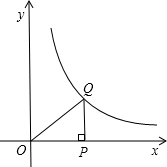    精英家教网如图，点P是x轴正半轴上一点，过点P作x轴的垂线交函数y=
    2
    x
    于点Q，连接OQ，当点P沿x轴方向运动时，Rt△OPQ的面积（　　）
    A、逐渐增大B、逐渐变小
    C、不变D、无法判断

    查看答案和解析>>

    （2013•沁阳市一模）以原点为圆心，1cm为半径的圆分别交x、y轴的正半轴于A、B两点，点P的坐标为（2，0）．
    （1）如图1，动点Q从点B处出发，沿圆周按顺时针方向匀速运动一周，设经过的时间为t秒，当t=1时，直线PQ恰好与⊙O第一次相切，连接OQ．求此时点Q的运动速度（结果保留）；
    （2）若点Q按照（1）中的方向和速度继续运动，
    ①当t为何值时，以O、P、Q为顶点的三角形是直角三角形；
    ②在①的条件下，如果直线PQ与⊙O相交，请求出直线PQ被⊙O所截的弦长．

    查看答案和解析>>

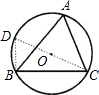    精英家教网阅读材料，解答问题：
    命题：如图，在锐角△ABC中，BC=a，CA=b，AB=c，△ABC的外接圆半径为R，则
    a
    sinA
    =
    b
    sinB
    =
    c
    sinC
    =2R．
    证明：连接CO并延长交⊙O于点D，连接DB，则∠D=∠A．
    因为CD是⊙O的直径，所以∠DBC=90°，
    在Rt△DBC中，sin∠D=
    BC
    DC
    =
    a
    2R
    ，
    所以sinA=
    a
    2R
    ，即
    a
    sinA
    =2R，
    同理：
    b
    sinB
    =2R，
    c
    sinC
    =2R，
    a
    sinA
    =
    b
    sinB
    =
    c
    sinC
    =2R，
    请阅读前面所给的命题和证明后，完成下面（1）（2）两题：
    （1）前面阅读材料中省略了“
    b
    sinB
    =2R，
    c
    sinC
    =2R”的证明过程，请你把“
    b
    sinB
    =2R”的证明过程补写出来．
    （2）直接运用阅读材料中命题的结论解题，已知锐角△ABC中，BC=
    		3
    ，CA=
    		2
    ，∠A=60°，求△ABC的外接圆半径R及∠C．
    精英家教网

    查看答案和解析>>

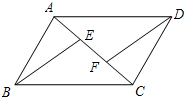    （2013•永嘉县一模）如图，E，F是平行四边形ABCD的对角线AC上的点，CE=AF．请你猜想：BE与DF有怎样的位置关系和数量关系？并对你的猜想加以证明：
    猜想：
    BE∥DF，BE=DF
    BE∥DF，BE=DF
    ；
    证明：
    连接BD，交AC于点O，连接DE，BF．
    ∵四边形ABCD是平行四边形，
    ∴BO=OD，AO=CO，
    又∵AF=CE，
    ∴AE=CF，
    ∴EO=FO，
    ∴四边形BEDF是平行四边形，
    ∴BE∥DF，BE=DF
    连接BD，交AC于点O，连接DE，BF．
    ∵四边形ABCD是平行四边形，
    ∴BO=OD，AO=CO，
    又∵AF=CE，
    ∴AE=CF，
    ∴EO=FO，
    ∴四边形BEDF是平行四边形，
    ∴BE∥DF，BE=DF
    ．

    查看答案和解析>>


    同步练习册答案