练习册

  • 练习册
  • 试题
    3．探讨在两圆外切或内切时.圆心距d与R和r之间的关系． Ⅴ．课后作业 习题3．9 Ⅵ．活动与探究 已知图中各圆两两相切.⊙O的半径为2R.⊙O1.⊙O2的半径为R.求⊙O3的半径． 分析:根据两圆相外切连心线的长为两半径之和.如果设⊙O3的半径为r.则O1O3＝O2O3＝R+r.连接OO3就有OO3⊥O1O2.所以OO2O3构成了直角三角形.利用勾股定理可求得⊙O3的半径r． 解:连接O2O3.OO3. ∴∠O2OO3＝90°.OO3＝2R-r. O2O3＝R+r.OO2＝R． ∴(R+r)2＝(2R-r)2+R2． ∴r＝R． 板书设计 §3．6 圆和圆的位置关系 【查看更多】

     

    题目列表(包括答案和解析)

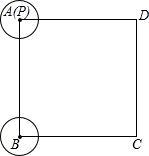    （2012•晋江市质检）如图，在正方形ABCD中，AB=6，半径为1的动圆⊙P从A点出发，以每秒3个单位的速度沿折线A-B-C-D向终点D移动，设移动的时间为t秒；同时，⊙B的半径r不断增大，且r=1+t（t≥0）．
    （1）当t=1.5秒时，两圆的位置关系是
    内切
    内切
    ；
    （2）当t≥4秒时，若两圆外切，则t的值为
    4或5.5
    4或5.5
    秒．

    查看答案和解析>>

    11、在矩形ABCD中，AB=8，AD=6，分别以A，C为圆心的两圆外切，且点D在⊙A内，点B在⊙A外，则⊙C半径r的取值范围是（　　）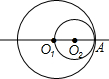

    查看答案和解析>>

    16、下列命题中假命题的是（　　）

    查看答案和解析>>

    如图，⊙O1、⊙O2内切于点A，其半径分别是6和3，将⊙O2沿直线O1O2平移至两圆外切时，则点O2移动的长度是（　　）

    查看答案和解析>>

    若两圆半径分别为R、r，圆心距为d，且d2-R2=r2+2Rr，则两圆的位置关系为
    内切或外切
    内切或外切
    ．

    查看答案和解析>>


    同步练习册答案