
题目列表(包括答案和解析)
(本题满分12分)在四边形ABCD中,AD=a,CD=b,点E在射线BA上,点F在射线BC上.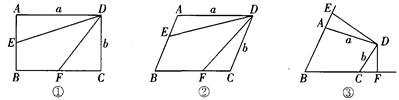
观察计算:
(1)如图①,若四边形ABCD是矩形,E是AB的中点.F是BC的中点,则四边形DEBF 的面积S四边形DEBF=_______.
(2)若四边形ABCD是平行四边形,E是AB的中点,F是BC的中点,则S四边形DEBF:S四边形ABCD=_______.
(3)如图②,若四边形ABCD是平行四边形,且BE:AB=2:3,BF:BC=2:3,则S四边形DEBF:S四边形ABCD=_______.
探索规律:
如图③,在四边形ABCD中,若BE:AB=n:m,BF:BC=n:m,试猜想S四边形DEBF:S四边形ABCD=_______,请说明理由.
解决问题:
如图④,某小区角落有一四边形空地,为了充分利用空间,美化环境,想把它沿两侧墙壁改造为一块绿地,使绿地面积是原空地面积的3倍.请分别在两侧墙壁上确定点E、F,画出改造线DE、DF,并写出作法.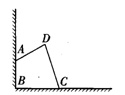
(本题满分12分)在四边形ABCD中,AD=a,CD=b,点E在射线BA上,点F在射线BC上.

观察计算:
(1)如图①,若四边形ABCD是矩形,E是AB的中点.F是BC的中点,则四边形DEBF 的面积S四边形DEBF=_______.
(2)若四边形ABCD是平行四边形,E是AB的中点,F是BC的中点,则S四边形DEBF:S四边形ABCD=_______.
(3)如图②,若四边形ABCD是平行四边形,且BE:AB=2:3,BF:BC=2:3,则S四边形DEBF:S四边形ABCD=_______.
探索规律:
如图③,在四边形ABCD中,若BE:AB=n:m,BF:BC=n:m,试猜想S四边形DEBF:S四边形ABCD=_______,请说明理由.
解决问题:
如图④,某小区角落有一四边形空地,为了充分利用空间,美化环境,想把它沿两侧墙壁改造为一块绿地,使绿地面积是原空地面积的3倍.请分别在两侧墙壁上确定点E、F,画出改造线DE、DF,并写出作法.

(本题满分12分)在四边形ABCD中,AD=a,CD=b,点E在射线BA上,点F在射线BC上.
观察计算:
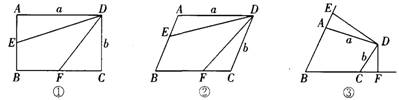
(1)如图①,若四边形ABCD是矩形,E是AB的中点.F是BC的中点,则四边形DEBF 的面积S四边形DEBF=_______.
(2)若四边形ABCD是平行四边形,E是AB的中点,F是BC的中点,则S四边形DEBF:S四边形ABCD=_______.
(3)如图②,若四边形ABCD是平行四边形,且BE:AB=2:3,BF:BC=2:3,则S四边形DEBF:S四边形ABCD=_______.
探索规律:
如图③,在四边形ABCD中,若BE:AB=n:m,BF:BC=n:m,试猜想S四边形DEBF:S四边形ABCD=_______,请说明理由.
解决问题:
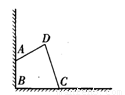
如图④,某小区角落有一四边形空地,为了充分利用空间,美化环境,想把它沿两侧墙壁改造为一块绿地,使绿地面积是原空地面积的3倍.请分别在两侧墙壁上确定点E、F,画出改造线DE、DF,并写出作法.
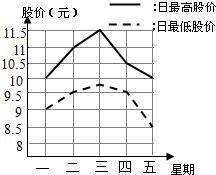 6、如图是某只股票从星期一至星期五每天的最高股价与最低股价的折线统计图,则这五天中最高股价与最低股价之差最大的一天是( )
6、如图是某只股票从星期一至星期五每天的最高股价与最低股价的折线统计图,则这五天中最高股价与最低股价之差最大的一天是( ) 4、如图是某厂连续7年产量增长率(相对于上年的增长率)统计图,仔细观察图形,下列说法正确的是( )
4、如图是某厂连续7年产量增长率(相对于上年的增长率)统计图,仔细观察图形,下列说法正确的是( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com