
题目列表(包括答案和解析)
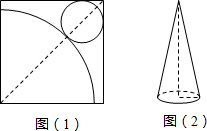 如图(1),在正方形铁皮上剪下一个圆形和扇形,使之恰好围成图(2)所示的一个圆锥模型,则圆的半径r与扇形的半径R之间的关系为( )
如图(1),在正方形铁皮上剪下一个圆形和扇形,使之恰好围成图(2)所示的一个圆锥模型,则圆的半径r与扇形的半径R之间的关系为( ) 如图,在正方形纸板上剪下一个扇形和圆,刚好能围成一个圆锥模型,设围成的圆锥底面半径为r,母线长为R,则r与R之间的关系为( )
如图,在正方形纸板上剪下一个扇形和圆,刚好能围成一个圆锥模型,设围成的圆锥底面半径为r,母线长为R,则r与R之间的关系为( )| A、R=2r | B、4R=9r | C、R=3r | D、R=4r |
 用一张扇形的纸片卷成一个如图所示的圆锥模型,要求圆锥的母线长为6cm,底面圆的直径为8cm,那么这张扇形纸片的圆心角度数是( )
用一张扇形的纸片卷成一个如图所示的圆锥模型,要求圆锥的母线长为6cm,底面圆的直径为8cm,那么这张扇形纸片的圆心角度数是( )| A、150° | B、180° | C、200° | D、240° |
| A、40πcm2 | B、20πcm2 | C、10πcm2 | D、5πcm2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com