
题目列表(包括答案和解析)
 一天,数学学习小组的三名同学小聪、小明、小雨发现一把30°的直角尺斜靠在教室的墙角(如图,△ABC中的直角边BC长为50cm),小聪提议针对这一现象,每人提出一个数学问题.
一天,数学学习小组的三名同学小聪、小明、小雨发现一把30°的直角尺斜靠在教室的墙角(如图,△ABC中的直角边BC长为50cm),小聪提议针对这一现象,每人提出一个数学问题. 一天,数学学习小组的三名同学小聪、小明、小雨发现一把30°的直角尺斜靠在教室的墙角(如图,△ABC中的直角边BC长为50cm),小聪提议针对这一现象,每人提出一个数学问题.
一天,数学学习小组的三名同学小聪、小明、小雨发现一把30°的直角尺斜靠在教室的墙角(如图,△ABC中的直角边BC长为50cm),小聪提议针对这一现象,每人提出一个数学问题.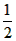 n(n+ 1),其中n是正整数。
n(n+ 1),其中n是正整数。 (1×2×3-0×1×2);
(1×2×3-0×1×2); (2×3×4-1×2×3);
(2×3×4-1×2×3);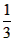 (3×4×5-2×3×4),
(3×4×5-2×3×4),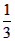 ×3×4×5=20。
×3×4×5=20。| 1 | 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com