
题目列表(包括答案和解析)
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.

(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD
向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于E
①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?
②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?
请直接写出相应的t值.
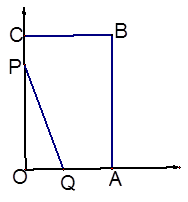
已知:在平面直角坐标系中矩形OABC如图,且A (6,0)、C(0,10),P点从C出发沿折线COA匀速运动、Q点从O出发沿折线OAB匀速运动,P、Q两点同时出发运动![]() 秒,且速度均为每秒2个单位长度,设
秒,且速度均为每秒2个单位长度,设![]() .
.
1.已知直线![]() 平分矩形OABC面积,求
平分矩形OABC面积,求![]() 的值;(经验之谈:过对称中心的任意一条直线均可将中心对称图形分成面积相等的两部分.)
的值;(经验之谈:过对称中心的任意一条直线均可将中心对称图形分成面积相等的两部分.)
2.当P点在CO上、Q点在OA上时,![]() 为何值有S=12.?
为何值有S=12.?
3.求在此运动过程中S与![]() 的函数关系式.
的函数关系式.
请同学们认真阅读下面材料,然后解答问题。(6分)
解方程(x2-1)2-5(x-1)+4=0
解:设y=x2-1
则原方程化为:y2-5y+4=0 ① ∴y1=1 y2=4
当y=1时,有x2-1=1,即x2=2 ∴x=±
当y=4时,有x2-1=4,即x2=5
∴x=±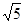
∴原方程的解为:x1=- x2=
x2= x3=-
x3=-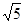 x4=
x4=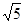
解答问题:
⑴填空:在由原方程得到①的过程中,利用________________法达到了降次的目的,体现了________________的数学思想。
⑵解方程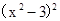 -3(
-3( -3)=0
-3)=0
已知:在平面直角坐标系中矩形OABC如图,且A (6,0)、C(0,10),P点从C出发沿折线COA匀速运动、Q点从O出发沿折线OAB匀速运动,P、Q两点同时出发运动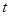 秒,且速度均为每秒2个单位长度,设
秒,且速度均为每秒2个单位长度,设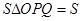 .
.
1.已知直线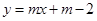 平分矩形OABC面积,求
平分矩形OABC面积,求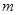 的值;(经验之谈:过对称中心的任意一条直线均可将中心对称图形分成面积相等的两部分.)
的值;(经验之谈:过对称中心的任意一条直线均可将中心对称图形分成面积相等的两部分.)
2.当P点在CO上、Q点在OA上时,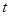 为何值有S=12.?
为何值有S=12.?
3.求在此运动过程中S与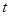 的函数关系式.
的函数关系式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com