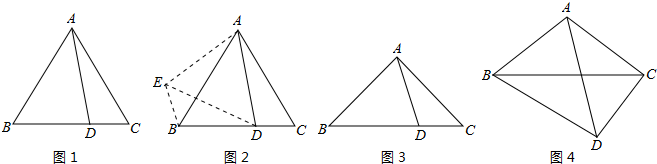
(2012•延庆县一模)如图1,已知:已知:等边△ABC,点D是边BC上一点(点D不与点B、点C重合),求证:BD+DC>AD.
下面的证法供你参考:
把△ACD绕点A顺时针旋转60°得到△ABE,连接ED,则有△ACD≌△ABE,DC=EB,∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,∴AD=DE.在△DBE中,BD+EB>DE,即:BD+DC>AD
实践探索:
(1)请你仿照上面的思路,探索解决下面的问题:
如图3,点D是等腰直角三角形△ABC边上的点(点D不与B、C重合).求证:BD+DC>
AD.
(2)如果点D运动到等腰直角三角形△ABC外或内时,BD、DC和AD之间又存在怎样的数量关系?直接写出结论.
创新应用:
(3)已知:如图4,等腰△ABC中,AB=AC,且∠BAC=α(α为钝角),D是等腰△ABC外一点,且∠BDC+∠BAC=180°,BD、DC与AD之间存在怎样的数量关系?写出你的猜想,并证明.

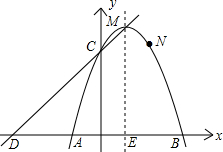 3)三点,且与y轴交于点C.
3)三点,且与y轴交于点C. ,
,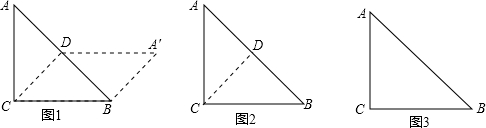

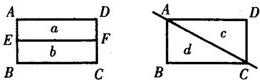 28、阅读下面操作过程,回答后面的问题:
28、阅读下面操作过程,回答后面的问题: