
题目列表(包括答案和解析)
| a |
| x |
| b |
| x-c |
在生活中不难发现这样的例子:三个量a,b和c之间存在着数量关系a=bc.例如:长方形面积=长×宽,匀速运动的路程=速度×时间.
(1)如果三个量a,b和c之间有着数量关系a=bc,那么:
①当a=0时,必须且只须 ;
②当b(或c)为非零定值时,a与c(或b)之间成 函数关系;
③当a(a≠0)为定值时,b与c之间成 函数关系.
(2)请你编一道有实际意义的应用性问题,解题所列的方程符合数量关系: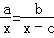 ,(其中x为未知数,a,b,c为已知数,不必解方程).
,(其中x为未知数,a,b,c为已知数,不必解方程).
在生活中不难发现这样的例子:三个量a,b和c之间存在着数量关系a=bc.例如:长方形面积=长×宽,匀速运动的路程=速度×时间.
(1)如果三个量a,b和c之间有着数量关系a=bc,那么:
①当a=0时,必须且只须 ;
②当b(或c)为非零定值时,a与c(或b)之间成 函数关系;
③当a(a≠0)为定值时,b与c之间成 函数关系.
(2)请你编一道有实际意义的应用性问题,解题所列的方程符合数量关系: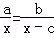 ,(其中x为未知数,a,b,c为已知数,不必解方程).
,(其中x为未知数,a,b,c为已知数,不必解方程).
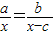 ,(其中x为未知数,a,b,c为已知数,不必解方程).
,(其中x为未知数,a,b,c为已知数,不必解方程).| a |
| x |
| b |
| x-c |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com