
题目列表(包括答案和解析)
| 已知:∠AOB=90。,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E。 (1)当三角板绕点C旋转到CD与OA垂直,CE与OB垂直时,(如图1) 此时由角平分线的性质可知CE=CD,又∵OM平分直角AOB,∴∠DOC=∠EOC=45。,∴△DCO与△ECO都为等腰直角三角形。∴OE=CE, OD=CD,又∵CE=CD,∴OE=OD=CD,请在此基础上继续证明: 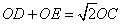 。 。(2)当三角板绕点C旋转到CD与OA不垂直时(如图2),上述结论是否还成立?试说明理由。 (3)当三角板绕点C旋转到图3位置上时,上述结论还成立吗?若不成立,请写出线段OD, OE, OC之间的关系。 |
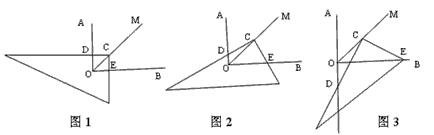 |
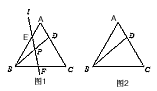
)如图1,Rt△ABC中AB = AC,点D、E是线段AC上两动点,且AD = EC,AM⊥BD,垂足为M,AM的延长线交BC于点N,直线BD与直线NE相交于点F。试判断△DEF的形状,并加以证明。
说明:⑴如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写
3步);⑵在你经历说明⑴的过程之后,可以从下列①、②中选取一个补充或更换已知条件,完成你的证明。
注意:选取①完成证明得
10分;选取②完成证明得5分。①画出将△
BAD沿BA方向平移BA长,然后顺时针旋转90°后图形;②点
K在线段BD上,且四边形AKNC为等腰梯形(AC∥KN,如图2)。附加题:如图3,若点D、E是直线AC上两动点,其他条件不变,试判断△DEF的形状,并说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com