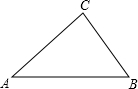
数学活动课上,甲、乙两位同学在研究一道数学题:“已知:如图1,在△ABC和△DEF中,∠A=∠D=90°,∠B=50°,∠E=32°,且BC=EF.试画直线m,l,使直线m将△ABC分成的两个小三角形与直线l将△DEF分成的两个小三角形分别相似,并标出每个小三角形各内角的度数.”
甲同学是这样做的:如图2,使得两个直角三角形的斜边重合,以斜边中点0为圆心,OB长为半径作出辅助圆,根据到定点的距离等于定长的点在圆上,可知A、B(E)、C(F)、D在⊙0上.设BD所在的直线m与AC所在的直线l交于点G,根据同弧所对的圆周角相等,由∠ABC=50°,∠DEF=32°,易求得∠ABG=DFG=18°,再由∠A=∠D=90°,可求得∠AGB=∠DGF=72°,∠GCB=40°,∠BGC=108°,从而△AGB∽△DGF.△GBC∽△GEF.
乙同学在甲同学的启发下,利用辅助圆又补充了其它分割方法.
你看明白甲同学的分割方法了吗?请你仿照甲同学的方法,把这道题其它的所有分割方法补充完整.

要求:不需写解答过程.如图2所示.利用辅助圆画出示意图,标明直线及每个小三角形各内角的度数即可.

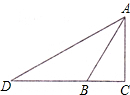
 14、(一题多解)如图所示,△ABC与△A′B′C′关于点O中心对称,但点O不慎被涂掉了,请你帮排版工人找到对称中心O的位置.
14、(一题多解)如图所示,△ABC与△A′B′C′关于点O中心对称,但点O不慎被涂掉了,请你帮排版工人找到对称中心O的位置.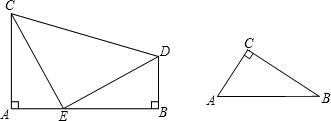
 甲题:已知x1、x2是关于x的一元二次方程x2-2x+a-1=0的两个实数根
甲题:已知x1、x2是关于x的一元二次方程x2-2x+a-1=0的两个实数根