
题目列表(包括答案和解析)
 9、一家电信公司给顾客提供两种上网收费方式:方式A以毎分0.1元的价格按上网所用时间计费;方式B除收月基费20元外,再以毎分0.05元的价格按上网所用时间计费.若上网所用时间为x分,计费为y元,如图,是在同一直角坐标系中,分别描述两种计费方式的函数的图象.有下列结论:
9、一家电信公司给顾客提供两种上网收费方式:方式A以毎分0.1元的价格按上网所用时间计费;方式B除收月基费20元外,再以毎分0.05元的价格按上网所用时间计费.若上网所用时间为x分,计费为y元,如图,是在同一直角坐标系中,分别描述两种计费方式的函数的图象.有下列结论:
一次函数 与反比例函数
与反比例函数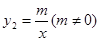 ,在同一直角坐标系中的图象如图所示,若
,在同一直角坐标系中的图象如图所示,若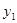 ﹥
﹥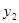 ,则x的取值范围是( )
,则x的取值范围是( )
A.-2﹤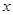 ﹤0或
﹤0或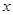 ﹥1? B.
﹥1? B.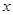 ﹤-2或0﹤
﹤-2或0﹤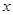 ﹤1
﹤1
C.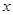 ﹥1 D.-2﹤
﹥1 D.-2﹤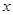 ﹤1
﹤1
一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网所用时间计费;方式B除收月基本费20元外,再以每分0.05元的价格按上网所用时间计费.若上网所用时间为x分,计费为y分,如图所示,是在同一直角坐标系中,分别描述两种计费方式的函数的图象,有下列结论:
①图象甲描述的是方式A;②图象乙描述的是方式B;③当上网所用时间为500分时,选择方式B省钱.其中,正确结论的个数是( )
A.3 B.2 C.1 D.0


一次函数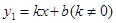 与反比例函数
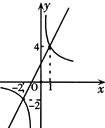
与反比例函数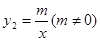 ,在同一直角坐标系中的图象如图所示,若
,在同一直角坐标系中的图象如图所示,若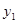 ﹥
﹥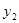 ,则x的取值范围是( )
,则x的取值范围是( )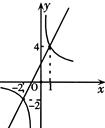
A.-2﹤ ﹤0或 ﹤0或 ﹥1? ﹥1? | B. ﹤-2或0﹤ ﹤-2或0﹤ ﹤1 ﹤1 |
C. ﹥1 ﹥1 | D.-2﹤ ﹤1 ﹤1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com