已知,A(3,a)是双曲线y=
上的点,O是原点,延长线段AO交双曲线于另一点B,又过B点作BK⊥x轴于K.
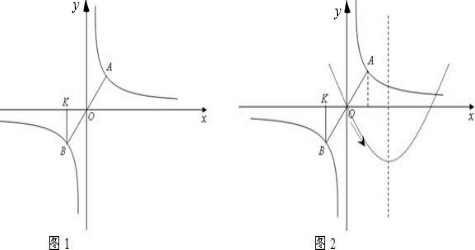
(1)试求a的值与点B坐标;
(2)在直角坐标系中,先使线段AB在x轴的正方向上平移6个单位,得线段A
1B
1,再依次在与y轴平行的方向上进行第二次平移,得线段A
2B
2,且可知两次平移中线段AB先后滑过的面积相等(即?AA
1B
1B与?A
1A
2B
2B
1的面积相等).求出满足条件的点A
2的坐标,并说明△AA
1A
2与△OBK是否相似的理由;
(3)设线段AB中点为M,又如果使线段AB与双曲线一起移动,且AB在平移时,M点始终在抛物线y=
(x-6)
2-6上,试判断线段AB在平移的过程中,动点A所在的函数图象的解析式;(无需过程,直接写出结果.)
(4)试探究:在(3)基础上,如果线段AB按如图2所示方向滑过的面积为24个平方单位,且M点始终在直线x=6的左侧,试求此时线段AB所在直线与x轴交点的坐标,以及M点的横坐标.

 已知反比例函数y=
已知反比例函数y=
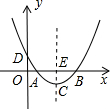 为6.
为6.