
题目列表(包括答案和解析)
A、反比例函数y=
| ||
B、反比例函数y=
| ||
C、经过反比例函数y=
| ||
D、反比例函数y=
|
A、反比例函数y=
| ||
B、反比例函数y=
| ||
C、反比例函数y=
| ||
D、反比例函数y=
|
下列关于反比例函数的叙述,不正确的是
A、反比例函数y= 的图象绕原点旋转180°后,能与原来的图象重合;
的图象绕原点旋转180°后,能与原来的图象重合;
B、反比例函数y= 的图象既不与x轴相交,也不与y轴相交;
的图象既不与x轴相交,也不与y轴相交;
C、经过反比例函数y= 的图象上任意一点向x轴,y轴作垂线,垂线段与坐标轴围成的矩形面积总等于
的图象上任意一点向x轴,y轴作垂线,垂线段与坐标轴围成的矩形面积总等于 ;
;
D、反比例函数y= ,当k>0时,y随x的增大而减少。
,当k>0时,y随x的增大而减少。
A.反比例函数y=
| ||
B.反比例函数y=
| ||
C.经过反比例函数y=
| ||
D.反比例函数y=
|
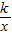 的图象绕原点旋转180°后,能与原来的图象重合
的图象绕原点旋转180°后,能与原来的图象重合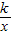 的图象既不与x轴相交,也不与y轴相交
的图象既不与x轴相交,也不与y轴相交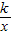 的图象上任意一点向x轴,y轴作垂线,垂线段与坐标轴围成的矩形面积总等于|k|
的图象上任意一点向x轴,y轴作垂线,垂线段与坐标轴围成的矩形面积总等于|k|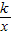 ,当k>0时,y随x的增大而减少
,当k>0时,y随x的增大而减少湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com