
题目列表(包括答案和解析)
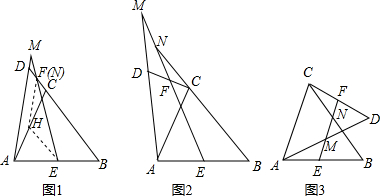 ∠BNE有何数量关系?请分别写出猜想,并任选一种情况证明.
∠BNE有何数量关系?请分别写出猜想,并任选一种情况证明. 24、如图(1)所示,AB∥CD,根据平行线的性质可知内错角∠B与∠C相等,观察图(2),(3)与(4),回答下列问题.
24、如图(1)所示,AB∥CD,根据平行线的性质可知内错角∠B与∠C相等,观察图(2),(3)与(4),回答下列问题.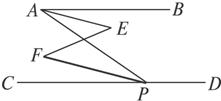 4、如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题小丽是这样证明的,请你将她的证明过程补充完整.
4、如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题小丽是这样证明的,请你将她的证明过程补充完整.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com