
题目列表(包括答案和解析)
如图
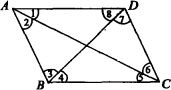
(1)已知AD∥BC,可以得出哪些角相等?为什么?
(2)已知AB∥DC,可以得出哪些角的和是180°?为什么?
(3)已知∠3=∠7,可以得出哪两条直线平行?为什么?
(4)已知∠1+∠2+∠3+∠4=180°,可以得出哪两条直线平行?为什么?
(5)由哪两条直线平行,可以得到∠4=∠8?为什么?
(6)由哪两条直线平行,可以得到∠3+∠4+∠5+∠6=180°?为什么?
如图

(1)已知AD∥BC,可以得出哪些角相等?为什么?
(2)已知AB∥DC,可以得出哪些角的和是180°?为什么?
(3)已知∠3=∠7,可以得出哪两条直线平行?为什么?
(4)已知∠1+∠2+∠3+∠4=180°,可以得出哪两条直线平行?为什么?
(5)由哪两条直线平行,可以得到∠4=∠8?为什么?
(6)由哪两条直线平行,可以得到∠3+∠4+∠5+∠6=180°?为什么?
 =
= 。
。 

 =
= ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似,现在B、D、C在一条直线,△ABD与△ADC不相似,需要考虑用别的方法换比。
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似,现在B、D、C在一条直线,△ABD与△ADC不相似,需要考虑用别的方法换比。 =
= 中,AC恰好是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰好是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明 =
= ,就可转化证
,就可转化证 =
= 。
。三角形内角平分线性质定理:三角形的内角平分线分对边所得的线段与两
边对应成比例。
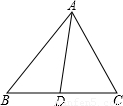
已知:如图,在△ABC中,AD是角平分线。
求证:![]() =
=![]() 。
。

分析:要证![]() =
=![]() ,一般只要证BD、DC与AB、AC
,一般只要证BD、DC与AB、AC
或BD、AB与DC、AC所在的三角形相似即可,现在点B、D、C
在一条直线上,△ABD与△ADC不相似,需要考虑用别的方法换比。在比例式![]()
=![]() 中,AC恰是BD、DC、AB的第四比例项,所以考虑过点C作CE//AD,交
中,AC恰是BD、DC、AB的第四比例项,所以考虑过点C作CE//AD,交
BA的延长线于点E,从而得到BD、DC、AB的第四比例项AE,这样,证明![]() =
=![]()
就可以转化成证AE=AC。
证明:过点C作CE//DA交BA的延长线于点E。
 。
。
(1)在上述证明过程中,用到了哪些定理?(写对两个定理即可)
(2)在上述分析、证明过程中,主要利用到了下列三种数学思想中的哪一种?选出一
个填在后面的括号内………………………………………………………………( )
A. 数形结合思想 B. 转化思想 C. 分类讨论思想
(3)用三角形内角平分线性质定理解答问题。
如下图,已知在△ABC中,AD是角平分线,AB=5cm,AC=4cm,
BC=7cm,求BD的长。

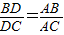
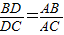 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式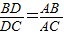 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明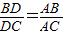 就可以转化成证AE=AC.
就可以转化成证AE=AC.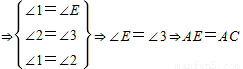 ,
,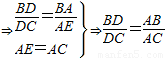

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com