
题目列表(包括答案和解析)

△ABC中,∠A=90°,点D在线段BC上(端点B除外),∠EDB = 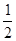 ∠C,BE⊥DE于点E,DE与AB相交于点F.
∠C,BE⊥DE于点E,DE与AB相交于点F.
(1)当AB = AC时(如图1)
①∠EBF= ▲ °;
②小明在探究过程中发现,线段FD 与BE始终保持一种特殊的数量关系,请你猜想这个关系,并利用所学知识证明猜想的正确性;
(2)探究:
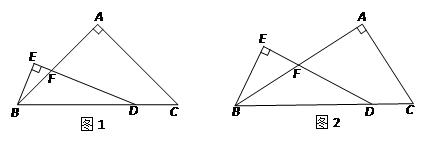
当AB = kAC时(k>0,如图2),用含k的式子表示线段FD与BE之间的数量关系,请直接写出结果.
【解析】(1)根据平行线的性质和全等三角形求证,(2)由(1)的结论可以直接写出
△ABC中,∠A=90°,点D在线段BC上(端点B除外),∠EDB = 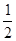 ∠C,BE⊥DE于点E,DE与AB相交于点F.
∠C,BE⊥DE于点E,DE与AB相交于点F.
(1)当AB = AC时(如图1)
①∠EBF= ▲ °;
②小明在探究过程中发现,线段FD 与BE始终保持一种特殊的数量关系,请你猜想这个关系,并利用所学知识证明猜想的正确性;
(2)探究:
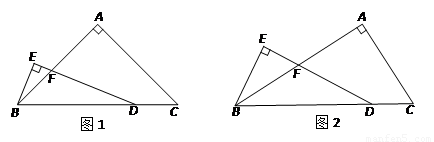
当AB = kAC时(k>0,如图2),用含k的式子表示线段FD与BE之间的数量关系,请直接写出结果.
【解析】(1)根据平行线的性质和全等三角形求证,(2)由(1)的结论可以直接写出
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com