
题目列表(包括答案和解析)
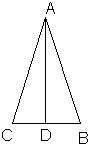 22、我们知道一个图形的性质和判定之间有着密切的联系.比如,由等腰三角形的性质“等边对等角”很易得到它的判定“等角对等边”.小明在学完“等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合”性质后,得到如下三个猜想:
22、我们知道一个图形的性质和判定之间有着密切的联系.比如,由等腰三角形的性质“等边对等角”很易得到它的判定“等角对等边”.小明在学完“等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合”性质后,得到如下三个猜想:【考点】全等三角形的判定与性质;直角梯形;旋转的性质.
【分析】过A作AN⊥BC于N,过E作EM⊥AD,交DA延长线于M,得出四边形ANCD是矩形,推出∠DAN=90°=∠ANB=∠MAN,AD=NC=5,AN=CD,求出BN=4,求出∠EAM=∠NAB,证△EAM≌△BNA,求出EM=BN=4,根据三角形的面积公式求出即可.
【解答】过A作AN⊥BC于N,过E作EM⊥AD,交DA延长线于M,
∵AD∥BC,∠C=90°,
∴∠C=∠ADC=∠ANC=90°,
∴四边形ANCD是矩形,
∴∠DAN=90°=∠ANB=∠MAN,AD=NC=5,AN=CD,
∴BN=9-5=4,
∵∠M=∠EAB=∠MAN=∠ANB=90°,
∴∠EAM+∠BAM=90°,∠MAB+∠NAB=90°,
∴∠EAM=∠NAB,
∵在△EAM和△BNA中,∠M=∠ANB;∠EAM=∠BAN;AE=AB,
∴△EAM≌△BNA(AAS),
∴EM=BN=4,
∴△ADE的面积是![]() ×AD×EM=
×AD×EM=![]() ×5×4=10.
×5×4=10.
故选A.
【点评】本题考查了矩形的性质和判定,三角形的面积,全等三角形的性质和判定,主要考查学生运用定理和性质进行推理的能力,题目比较好,难度适中.
 我们知道一个图形的性质和判定之间有着密切的联系.比如,由等腰三角形的性质“等边对等角”很易得到它的判定“等角对等边”.小明在学完“等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合”性质后,得到如下三个猜想:
我们知道一个图形的性质和判定之间有着密切的联系.比如,由等腰三角形的性质“等边对等角”很易得到它的判定“等角对等边”.小明在学完“等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合”性质后,得到如下三个猜想: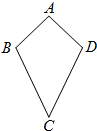 来逐步认识四边形;
来逐步认识四边形;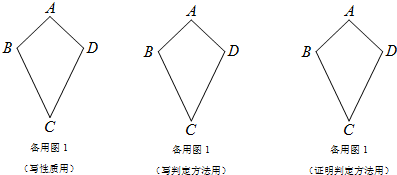
(11·佛山)阅读材料
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;
比如我们通过学习两类特殊的四边形,即平行四边形和梯形(继续学习它们的特殊类型如矩形、等腰梯形等)来逐步认识四边形;
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=CD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com