
题目列表(包括答案和解析)
实践与探究:如图,已知 中,
中, 厘米,
厘米, 厘米,点
厘米,点 为
为 的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)用含有t的代数式表示CP
(2)若点Q的运动速度与点P的运动速度相等,经过1秒后, 与
与 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使 与
与 全等?
全等?
实践与探究:如图,已知 中,
中, 厘米,
厘米, 厘米,点
厘米,点 为
为 的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
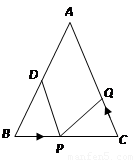
(1)用含有t的代数式表示CP
(2)若点Q的运动速度与点P的运动速度相等,经过1秒后, 与
与 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使 与
与 全等?
全等?
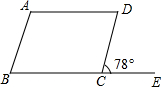 (要写出过程与理由)如图,已知AB∥CD,BE∥AD,∠DCE=78°,求∠A、∠B、∠D的度数.
(要写出过程与理由)如图,已知AB∥CD,BE∥AD,∠DCE=78°,求∠A、∠B、∠D的度数.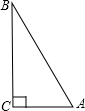
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com