
题目列表(包括答案和解析)
| ||
| 3 |
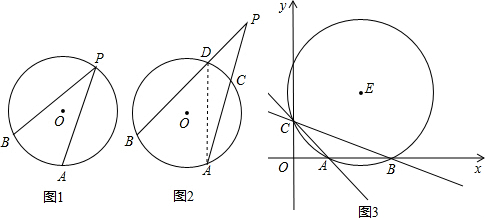
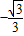 x+2相交于y轴上的点C,与x轴分别交于点A、B.经过A、B、C三点作⊙E,点P是第一象限内⊙E外的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,
x+2相交于y轴上的点C,与x轴分别交于点A、B.经过A、B、C三点作⊙E,点P是第一象限内⊙E外的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,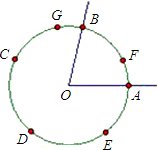 只用圆规度量∠XOY的度数,方法是:以顶点O为圆心任意画一个圆,与角的两边分别交于点A,B(如图),在这个圆上顺次截取
只用圆规度量∠XOY的度数,方法是:以顶点O为圆心任意画一个圆,与角的两边分别交于点A,B(如图),在这个圆上顺次截取 =
= =
= =
= =
= =…这样绕着圆一周周地截下去,直到绕第n周时,终于使第m次截得的弧的末端恰好与点A重合(m>n),那么∠XOY的度数等于________.
=…这样绕着圆一周周地截下去,直到绕第n周时,终于使第m次截得的弧的末端恰好与点A重合(m>n),那么∠XOY的度数等于________.如图,已知半圆![]() 的直径
的直径![]() ,将一
,将一![]() 个三角板的直角顶点固定在圆心
个三角板的直角顶点固定在圆心![]() 上,当三角板绕着点
上,当三角板绕着点![]() 转动时,三角板的两条直角边与半圆圆周分别交于
转动时,三角板的两条直角边与半圆圆周分别交于![]() 、
、![]() 两点,连结
两点,连结![]() 、
、
![]() 交于点
交于点![]() .
.
(1) 求证:![]() ;
;
(2) 求证:![]() 恒成立;
恒成立;
(3) 设![]() ,求
,求![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
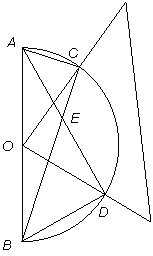
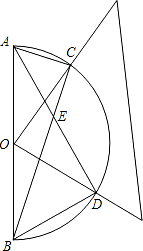 直角边与半圆圆周分别交于C、D两点,连接AD、BC交于点E.
直角边与半圆圆周分别交于C、D两点,连接AD、BC交于点E.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com