
题目列表(包括答案和解析)
顶点在圆上,并且两边都与圆还有另一个交点的角叫做
________.定理:一条弧所对的圆周角等于它所对圆心角的
________.推论
1:在________中,同弧或________所对的圆周角________,相等的圆周角所对的弧也________.推论
2:半圆或直径所对的圆周角是________;90°的圆周角所对的弦是________. ,它是一个无理数.
,它是一个无理数.


 的线段吗?
的线段吗?
 的点吗?
的点吗?
| 2 |


| 5 |
| 5 |

| 10 |

| 5 |

 ,它是一个无理数.
,它是一个无理数.
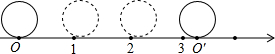

 的线段吗?
的线段吗?
 的点吗?
的点吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com