24、如图，△ABC经过一次平移到△DFE的位置，请回答下列问题：
（1）点C的对应点是点，∠D=，BC=；
（2）连接CE，那么平移的方向就是的方向，平移的距离就是线段的长度，可量出约为cm；
（3）连接AD、BF、BE，与线段CE相等的线段有．

如图，△ABC经过一次平移到△DFE的位置，请回答下列问题：



（1）点C的对应点是点______，∠D=______，BC=______；
（2）连接CE，那么平移的方向就是______的方向，平移的距离就是线段______的长度，可量出约为______cm；
（3）连接AD、BF、BE，与线段CE相等的线段有______．

24、阅读材料，并回答下列问题：
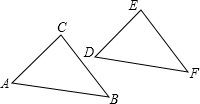
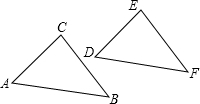
如图1，以AB为轴，把△ABC翻折180°，可以变换到△ABD的位置；如图2，把△ABC沿射线AC平移，可以变换到△DEF的位置．像这样，其中的一个三角形是另一个三角形经翻折、平移等方法变换成的，这种只改变位置，不改变形状大小的图形变换，叫三角形的全等变换．
（1）请你写出一种全等变换的方法（除翻折、平移外）．；
（2）如图2，△ABC沿射线AC平移到△DEF，若平移的距离为2，且AC=3，则DC=；
（3）如图3，D、E分别是△ABC的边AB、AC上的点，把△ADE沿DE翻折，当点A落在四边形BCED内部变为F时，则∠F和∠BDF+∠CEF之间的数量关系始终保持不变，请你直接写出它们之间的关系式：．