
题目列表(包括答案和解析)
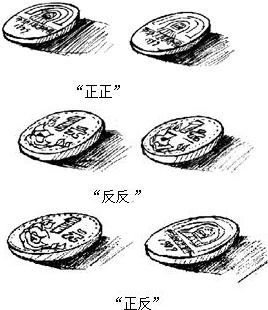
掷两枚硬币,规定落地后,国徽朝上为正,国徽朝下为“反”,则会出现以下三种情况.



分别求出每种情况的概率.
(1)小刚做法:通过列表可知,每种情况都出现一次,因此各种情况发生的概率均占 .
.
|
可能出现的情况 |
正正 |
正反 |
反反 |
|
概率 |
|
|
|

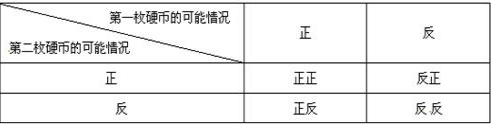
小敏的做法:
|
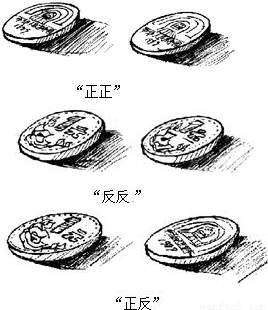
第一枚硬币的可能情况 第二枚硬币的可能情况 |
正 |
反 |
|
正 |
正正 |
反正 |
|
反 |
正反 |
反反 |
通过以上列表,小敏得出:“正正”的情况发生概率为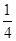 .“正反”的情况发生的概率为
.“正反”的情况发生的概率为 ,“反反”的情况发生的概率为
,“反反”的情况发生的概率为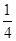 .
.
(1)以上三种做法,你同意哪种,说明你的理由;
(2)用列表法求概率时要注意哪些?
 .
.

 ,“正反”的情况发生的概率为
,“正反”的情况发生的概率为 ,“反反”的情况发生的概率为
,“反反”的情况发生的概率为 .
.| 掷两枚硬币,规定落地后,国徽朝上为“正”,国徽朝下为“反”,则会出现以下三种情况: | ||||||||
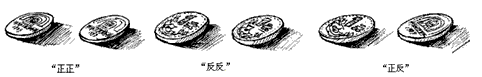 | ||||||||
| 分别求出每种情况的概率。 | ||||||||
①小刚的做法:通过列表可知,每种情况都出现一次,因此各种情况发生的概率均占 。 。 | ||||||||
| ||||||||
 | ||||||||
| ③小敏的做法: | ||||||||
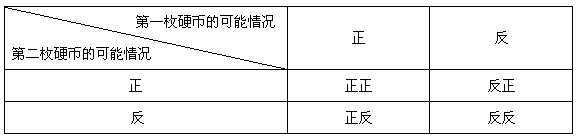 | ||||||||
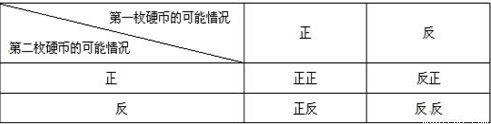
通过以上列表,小敏得出:“正正”的情况发生概率为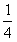 ,“正反”的情况发生的概率为 ,“正反”的情况发生的概率为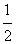 ,“反反”的情况发生的概率为 ,“反反”的情况发生的概率为 。 。(1)以上三种做法,你同意哪种,说明你的理由; (2)用列表法求概率时要注意哪些? |
 .
.

 ,“正反”的情况发生的概率为
,“正反”的情况发生的概率为 ,“反反”的情况发生的概率为
,“反反”的情况发生的概率为 .
.| x(元) | 100 | 200 | 300 | … | |
| y(亩) | 800 | 1600 | 2400 | 3200 | … |
| z(元) | 3000 | 2700 | 2400 | 2100 | … |
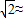 1.414)
1.414)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com