
题目列表(包括答案和解析)
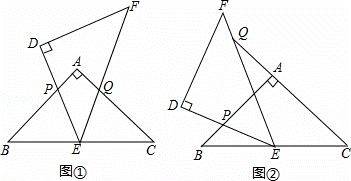
如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=![]() ,CQ=
,CQ=![]() 时,P、Q两点间的距离 (用含
时,P、Q两点间的距离 (用含![]() 的代数式表示).新 课 标 第一网
的代数式表示).新 课 标 第一网
如图,矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米(
厘米(![]() ).动点
).动点![]() 同时从
同时从![]() 点出发,分别沿
点出发,分别沿![]() ,
,![]() 运动,速度是
运动,速度是![]() 厘米/秒.过
厘米/秒.过![]() 作直线垂直于
作直线垂直于![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() .当点
.当点![]() 到达终点
到达终点![]() 时,点
时,点![]() 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为![]() 秒.新 课 标 第 一 网
秒.新 课 标 第 一 网
(1)若![]() 厘米,
厘米,![]() 秒,则
秒,则![]() ______厘米;
______厘米;
(2)若![]() 厘米,求时间
厘米,求时间![]() ,使
,使![]() ,并求出它们的相似比;
,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形![]() 与梯形
与梯形![]() 的面积相等,求
的面积相等,求![]() 的取值范围;
的取值范围;
(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形![]() ,梯形
,梯形![]() ,梯形
,梯形![]() 的面积都相等?若存在,求
的面积都相等?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 |
已知抛物线C1的函数解析式为y=ax2+bx-3a(b<0),若抛物线C1经过点(0,-3),方程ax2+bx-3a=0的两根为x1,x2,且|x1-x2|=4.
⑴求抛物线C1的顶点坐标. 新 课 标 第 一 网
⑵已知实数x>0,请证明x+![]() ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+![]() =2.
=2.
⑶若将抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线C2,设A(m,y1),B(n,y2)是C2上的两个不同点,且满足:∠AOB=90︒,m>0,n<0.请你用含m的表达式表示出△AOB的面积S,并求出S的最小值及S取最小值时一次函数OA的函数解析式.
(参考公式:在平面直角坐标系中,若P(x1,y1),Q(x2,y2),则P,Q两点间的距离为![]() )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com