
题目列表(包括答案和解析)
| b |
| a |
| c |
| a |
| b |
| 2a |
| b |
| a |
| b |
| 2a |
| c |
| a |
| b |
| 2a |
| b |
| 2a |
| b2-4ac |
| 4a |
| b |
| a |
| c |
| a |
| b |
| 2a |
| b |
| a |
| b |
| 2a |
| c |
| a |
| b |
| 2a |
| b |
| 2a |
| b2-4ac |
| 4a |
先阅读,再解题.
用配方法解一元二次方程 (a≠0)如下:
(a≠0)如下:
移项,得 ,
,
方程两边除以a,得 .
.
方程两边加上 ,得
,得 ,即
,即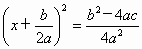 .
.
因为a≠0,所以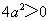 ,从而当
,从而当 时,方程右边是一个正数,正数的平方根有两个,因此方程有两个不相等的实数根;当
时,方程右边是一个正数,正数的平方根有两个,因此方程有两个不相等的实数根;当 时,方程右边是零,因此方程有两个相等的实数根;当
时,方程右边是零,因此方程有两个相等的实数根;当 时,方程右边是一个负数,而负数没有平方根,因此方程没有实数根.所以我们可以根据
时,方程右边是一个负数,而负数没有平方根,因此方程没有实数根.所以我们可以根据 的值来判断方程的根的情况,请利用上述论断,不解方程,判别方程
的值来判断方程的根的情况,请利用上述论断,不解方程,判别方程 的根的情况.
的根的情况.
苏科版教材中有这样一句话:“一般地,如果二次函数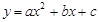 的图象与x轴有两个公共点,那么一元二次方程
的图象与x轴有两个公共点,那么一元二次方程 有两个不相等的实数根.”据此判断方程x2-2x=
有两个不相等的实数根.”据此判断方程x2-2x= -2实数根的情况是 ( )
-2实数根的情况是 ( )
| A.有三个实数根 | B.有两个实数根 | C.有一个实数根 | D.无实数根 |
 的图象与x轴有两个公共点,那么一元二次方程
的图象与x轴有两个公共点,那么一元二次方程 有两个不相等的实数根.”据此判断方程x2-2x=
有两个不相等的实数根.”据此判断方程x2-2x= -2实数根的情况是 ( )
-2实数根的情况是 ( )| A.有三个实数根 | B.有两个实数根 | C.有一个实数根 | D.无实数根 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com