练习册

  • 练习册
  • 试题
    平行线的概念.性质和画法 【查看更多】

     

    题目列表(包括答案和解析)

    知识回顾：我们在学习《二次根式》这一章时，对二次根式有意义的条件、性质和运算法则进行了探索，得到了如下结论：
    （1）二次根式
    		a
    有意义的条件是a≥0．
    （2）二次根式的性质：①（
    		a
    ）2=a（a≥0）；②
    		a2
    =|a|．
    （3）二次根式的运算法则：
    ①
    		a
    •
    		b
    =
    		ab
    （a≥0，b≥0）；
    ②
    		a
    		b
    =
    a
    b
    （a≥0，b＞0）；
    ③a
    		c
    ±b
    		c
    =（a±b）
    		c
    （c≥0）．
    类比推广：根据探索二次根式相关知识过程中获得的经验，解决下面的问题．
    （1）写出n次根式
    na
    （n≥3，n是整数）有意义的条件和性质；
    （2）计算
    3-16
    +
    32
    ．

    查看答案和解析>>

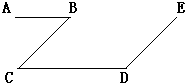    21、如图，给出下列三个论断：①∠B+∠D=180°；②AB∥CD；③BC∥DE．请你以其中两个论断作为已知条件，填入“已知”栏中，以一个论断作为结论，填入“结论栏中，使之成为一道由已知可得到结论的题目，并说明理由．
    已知，如图，
    ①②
    ，
    结论：
    ③
    ．
    理由：
    平行线的判定与性质
    ．

    查看答案和解析>>

    下列语句中是命题的是


    1. A.
      延长线段AB到点C，使AC＝2BC
    2. B.
      你能说出平行线的三条性质吗
    3. C.
      所有的角都相等
    4. D.
      简单的习题

    查看答案和解析>>

    （2013•绵阳）我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心．重心有很多美妙的性质，如关于线段比．面积比就有一些“漂亮”结论，利用这些性质可以解决三角形中的若干问题．请你利用重心的概念完成如下问题：
    （1）若O是△ABC的重心（如图1），连结AO并延长交BC于D，证明：
    AO
    AD
    =
    2
    3
    ；
    （2）若AD是△ABC的一条中线（如图2），O是AD上一点，且满足
    AO
    AD
    =
    2
    3
    ，试判断O是△ABC的重心吗？如果是，请证明；如果不是，请说明理由；
    （3）若O是△ABC的重心，过O的一条直线分别与AB、AC相交于G、H（均不与△ABC的顶点重合）（如图3），S四边形BCHG，S△AGH分别表示四边形BCHG和△AGH的面积，试探究
    S四边形BCHG
    S△AGH
    的最大值．

    查看答案和解析>>

    我们所学的几何知识可以理解为对“构图”的研究：根据给定的（或构造的）几何图形提出相关的概念和问题（或者根据问题构造图形），并加以研究．
    例如：在平面上根据两条直线的各种构图，可以提出“两条直线平行”、“两条直线相交”的概念；若增加第三条直线，则可以提出并研究“两条直线平行的判定和性质”等问题（包括研究的思想和方法）．
    请你用上面的思想和方法对下面关于圆的问题进行研究：
    （1）如图1，在圆O所在平面上，放置一条直线m（m和圆O分别交于点A、B），根据这个图形可以提出的概念或问题有哪些？（直接写出两个即可）
    （2）如图2，在圆O所在平面上，请你放置与圆O都相交且不同时经过圆心的两条直线m和n（m与圆O分别交于点A、B，n与圆O分别交于点C、D）．请你根据所构造的图形提出一个结论，并证明之；
    （3）如图3，其中AB是圆O的直径，AC是弦，D是
    		ABC
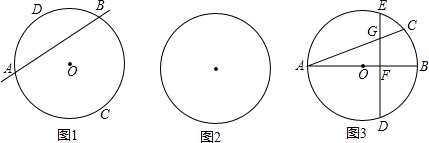    的中点，弦DE精英家教网⊥AB于点F．请找出点C和点E重合的条件，并说明理由．

    查看答案和解析>>


    同步练习册答案