
题目列表(包括答案和解析)
将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°。
【小题1】(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点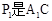 与AB的交点,点Q是
与AB的交点,点Q是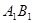 与BC的交点,求证:
与BC的交点,求证: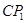 =
=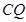 ;
;
【小题2】(2)在图2中,若AP1= ,则CQ等于多少?
,则CQ等于多少?
【小题3】(3)将图2中△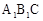 绕点C顺时针旋转到△
绕点C顺时针旋转到△ (如图3),点
(如图3),点 与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段
与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段 之间存在一个怎样的数量关系?.
之间存在一个怎样的数量关系?.
△ABC中,射线AD平分∠BAC,AD交边BC于E点.
(1)如图1,若AB=AC,∠BAC=90°,则 ( )
( ) ;
;

(2)如图2,若AB≠AC,则(1)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由;

(3)如图3,若AB>AC,∠BAC=∠BDC=90°,∠ABD为锐角,DH⊥AB于H,则线段AB、AC、BH之间的数量关系是( ),并证明.

如图所示,BC=1,数轴上点A所表示的数为a,则a值为( )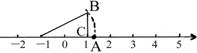
A.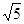 +1 +1 | B.-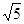 +1 +1 | C.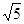 -1 -1 | D.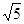 |
如图所示,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.求∠PAQ的度数.
如图,在△ABC中,∠A=30º,AB=2.则BC=????? .

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com