如图的格点图中,每行(列)相邻两个格点之间都相距1个长度单位.
(1)如图,格点C与格点A、B构成的三角形ABC的面积是2,还有一些格点与格点A、B构成的三角形面积也是2,请找出所有这样的格点,并在图上标示出来.

(2)有些格点与格点A、B可以构成等腰三角形ABD,请你找出所有这样的格点D,并在图中标出.

(3)问题(2)所得到的等腰三角形中有没有等边三角形?如有,将它们标示出来;
如没有,思考:在下面的8*8格点图中,是否存在以格点为顶点的等边三角形,如果存在,请标示出来,如果不存在,说明理由,一般地,对于任意大的格点图(如100*100个点的格点图),这个结论是否成立?

(4)问题(2)所得到的等腰三角形中有没有以AB为腰的等腰直角三角形,有没有以AB为底的等腰直角三角形?
一般地,在充分大的格点图中,对于任意给定的两个格点,是否一定存在以这两个格点所在线段为腰的等腰直角三角形?如果一定有,说明你的构造方法;如果不一定有,思考:对于什么样的两点(即两点的坐标之间满足什么条件时)有.
在充分大的格点图中,对于任意给定的两个格点,是否一定存在以这两个格点所在线段为底的等腰直角三角形?如果一定有,说明你的构造方法;如果不一定有,思考:对于什么样的两点(即两点的坐标之间满足什么条件时)有.

 如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作:
如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作: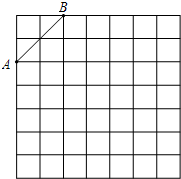 如图,是7×7的正方形网格,请在所给网格中按下列要求操作:
如图,是7×7的正方形网格,请在所给网格中按下列要求操作:

