
题目列表(包括答案和解析)
阅读下面的文字,然后回答问题.

我们知道三角形的内角和为180°,我们可以利用这一结论求得四边形的内角和,如图,已知四边形ABCD,求四边形ABCD的内角和.
解:在四边形ABCD的内部任取一点O,连结AO,BO,CO,DO,则有四个三角形的ABO,BCO,CDO,DAO,其内角和共为:180°×4=720°.又∵∠1+∠2+∠3+∠4=360°,∴∠ABC+∠BCD+∠CDA+∠DAB=720°-360°=360°,即四边形的内角和为360°.
问题:(1)在上述解题过程中,运用了________数学思想.
(2)你能用上述方法,求出五边形的内角和吗?
(3)n边形的内角和是多少呢?
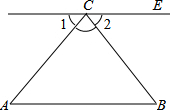 如何说明三角形内角和是180°?
如何说明三角形内角和是180°?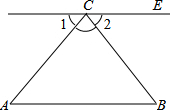

| 1 |
| 2 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com