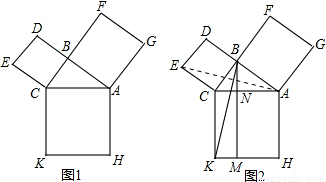
在研究勾股定理时,同学们都见到过图1,∠CBA=90°,四边形ACKH、BCED、ABFG都是正方形.
(1)连接BK、AE得到图2,则△CBK≌△CEA,此时两个三角形全等的判定依据是______;过B作BM⊥KH于M,交AC于N,则S
矩形KMNC=2S
△CKB;同理S
正方形BCED=2S
△CEA,得S
正方形BCED=S
矩形KMNC,然后可证得勾股定理.
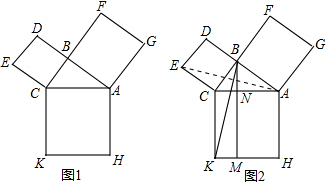
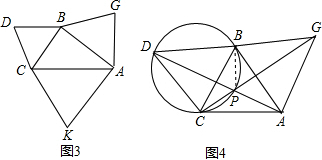
(2)在图1中,若将三个正方形“退化”为正三角形,得到图3,同学们可以探究△BCD、△ABG、△ACK的面积关系是______.
(3)为了研究问题的需要,将图1中的Rt△ABC也进行“退化”为锐角△ABC,并擦去正方形ACKH得图4,由AB、BC两边向三角形外作正△BCD、正△ABG,△BCD的外接圆与AD交于点P,此时C、P、G共线,从△ABC内一点到A、B、C三个顶点的距离之和最小的点恰为点P(已经被他人证明).设BC=3,CA=4,∠BCA=60°.求PA+PB+PC的值.