
题目列表(包括答案和解析)
 其中一边就利用院子里的围墙.已知市场上竹篱笆每米8元.
其中一边就利用院子里的围墙.已知市场上竹篱笆每米8元.

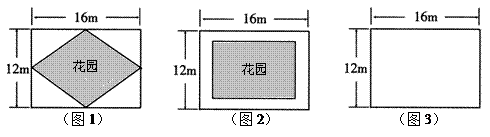
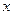 的值;
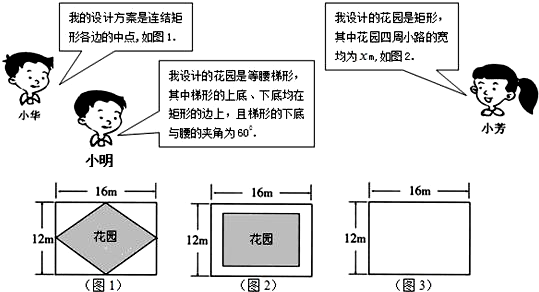
的值;在一块长16m,宽12m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,且整体图案成轴对称图形.下面是小华、小芳与小明的设计方案.
请你根据以上的对话,完成下列问题.
(1)你认为小华所设计的花园的形状是 ,整个设计图案共有 条对称轴;
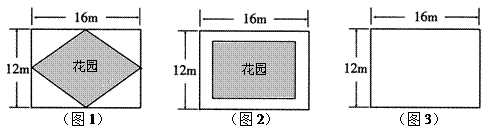
(2)请你帮助小芳计算出道路的宽度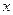 的值;
的值;
(3)请你根据小明的设计方案在图3中画出符合设计条件的草图,然后根据你所画的草图求出该等腰梯形的上底和下底的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com