(2007•东城区二模)阅读理解下列例题:
例题:解一元二次不等式x
2-2x-3<0.
分析:求解一元二次不等式时,应把它转化成一元一次不等式组求解.
解:把二次三项式x
2-2x-3分解因式,得:x
2-2x-3=(x-1)
2-4=(x-3)(x+1),又x
2-2x-3<0,
∴(x-3)(x+1)<0.
由“两实数相乘,同号得正,异号得负”,得
①或
②
由①,得不等式组无解;由②,得-1<x<3.
∴(x-3)(x+1)<0的解集是-1<x<3.
∴原不等式的解集是-1<x<3.
(1)仿照上面的解法解不等式x
2+4x-12>0.
(2)汽车在行驶中,由于惯性作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”,刹车距离是分析事故的一个重要因素.某车行驶在一个限速为40千米/时的弯道上,突然发现异常,马上刹车,但是还是与前面的车发生了追尾,事故后现场测得此车的刹车距离略超过10米,我们知道此款车型的刹车距离S(米)与车速x(千米/时)满足函数关系:S=ax
2+bx,且刹车距离S(米)与车速x(千米/时)的对应值表如下:
| 车速x(千米/时) |
30 |
50 |
70 |
… |
| 刹车距离S(米) |
6 |
15 |
28 |
… |
问该车是否超速行驶?

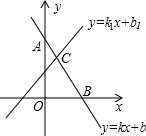 在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:
在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下: