阅读下面的文字,完成下列各题。(8分)
我们平时所熟悉的污染物,多是“物质流污染物”,如粉尘、废水、毒物、固体废弃物等,它们可见可闻,容易被人感知。而“能量流污染物”就不同了,如电离辐射、电磁辐射、次声等,其特点是看不见、闻不到、摸不着,不占空间,也不留痕迹,更不易被人感知。
“能量流污染物”中的电磁辐射,是一种从电磁源向外发出电磁能量的现象。换句话说,电磁辐射借辐射现象传递能量。太阳发出光和热,就是如此。电磁辐射与我们日常生活的联系最为密切。地球本身就是一个大磁场,其表面的热辐射和雷电都可产生电磁辐射。我们身边的任何电子、电器设备在运行时,也会产生一定强度的电磁辐射。可见,不论在何处,我们都会受到许多不同频率的电场和磁场的复合照射,它们都可以产生各种形式、不同频率、不同强度的电磁污染。
研究表明,长期暴露在高强度的电磁场中,可能增加癌症发病的概率,也有可能引起人体染色体的畸变。这是因为人体生命活动包含一系列的生物电活动,这些生物电对环境的电磁波非常敏感,当人体接受电磁辐射时,体内分子会随着电磁场的转换快速运动,使体温升高,进而引起中枢神经和植物精神系统的功能障碍。即使吸收辐射不足以引起体温增高,也会对脑细胞产生影响,使大脑皮质细胞活动能力减弱,已形成的条件反射受到抑制。如果机体过多或过久地暴露于电磁辐射的环境中,就会“受激”而产生不利的生物效应,出现急性损害或慢性损害。平时电磁辐射的慢性损害比较多见,且是以功能性危害的表现为主,器质性损害的表现较少。受到电磁辐射污染,一般会出现头疼、失眠、记忆衰退、心律不齐等中枢神经的问题,也会出现皮肤病以及视力下降等现象。正处于生长发育阶段的儿童,神经系统和免疫系统尚未成熟,发育组织的生理活动十分活跃,所以更容易受到电磁辐射的伤害。
为了减少电磁辐射的伤害,在日常生活中应该注意自我防护。远离辐射源,尽量缩短使用电器的时间,适当多吃一些富含维生素A、C和蛋白质的食物。
【小题1】下列说法不符合文意的一项是(3分)
| A.在日常生活中,那些不易被人感知的电离辐射、电磁辐射、次声等都属于“能量流污染物”。 |
| B.太阳发出光发热,也是一种电磁辐射现象,不仅产生电磁能量,也产生电磁污染。 |
| C.电磁辐射污染带来的头疼、失眠、皮肤病等问题,都是电磁辐射对人体造成的器质性损害。 |
| D.电磁辐射对人体的损害程度与人的神经系统和免疫系统的发育程度是密切相关的。 |
【小题2】在生活中,为什么对“电磁污染”必须给予足够的重视?(5分)

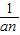 (a≠O).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了.例如a2•a-3=a2+(-3)=a-1=
(a≠O).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了.例如a2•a-3=a2+(-3)=a-1=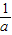 .数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+
.数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+ i=
i= i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6•0.5i=3i; 2i•3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±
i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6•0.5i=3i; 2i•3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±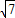 i.…数的不断发展进一步证实,这种规定是合理的.
i.…数的不断发展进一步证实,这种规定是合理的.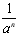 (a≠0).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了。例如a2·a-3=a2+(-3)=a-1=
(a≠0).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了。例如a2·a-3=a2+(-3)=a-1=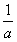 ,数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+
,数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+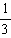 i=
i=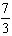 i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6·0.5i=3i;2i·3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±
i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6·0.5i=3i;2i·3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±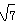 i.…数的不断发展进一步证实,这种规定是合理的.试用配方法求一元二次方程x2+x+1=0的非实数解:
i.…数的不断发展进一步证实,这种规定是合理的.试用配方法求一元二次方程x2+x+1=0的非实数解: 