
题目列表(包括答案和解析)
数学活动——求重叠部分的面积。
问题情境:数学活动课上,老师出示了一个问题:

如图(1),将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE经过点C,DF交AC于点G。
求重叠部分(△DCG)的面积。
(1)独立思考:请解答老师提出的问题。
(2)合作交流:“希望”小组受此问题的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图(2),你能求出重叠部分(△DGH)的面积吗?请写出解答过程。
(3)提出问题:老师要求各小组向“希望”小组学习,将△DEF绕点D旋转,再提出一个求重叠部分面积的问题。“爱心”小组提出的问题是:如图(3),将△DEF绕点D旋转,DE,DF分别交AC于点M,N,使DM=MN,求重叠部分(△DMN)的面积。
任务:①请解决“爱心”小组所提出的问题,直接写出△DMN的面积是 .
②请你仿照以上两个小组,大胆提出一个符合老师要求的问题,并在图中画出图形,标明字母,不必解答(注:也可在图(1)的基础上按顺时针方向旋转)。
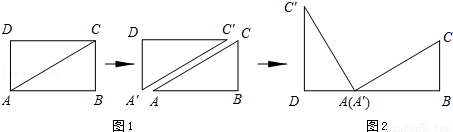
情境观察将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是 _________ ,∠CAC′= _________ °.
问题探究
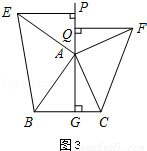
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
拓展延伸
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.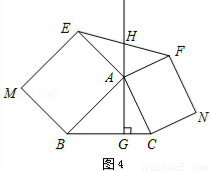
情境观察将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是 _________ ,∠CAC′= _________ °.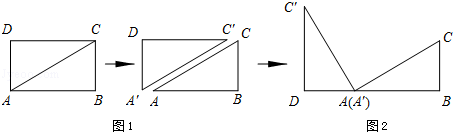
问题探究
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.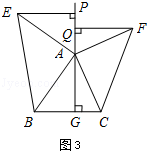
拓展延伸
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.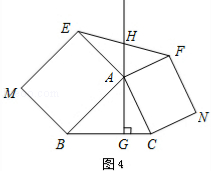
设计调查问卷时要注意( )
①问题应尽量简明;②不要提问被调查者不愿意回答的问题;③提问不能涉及提问者的个人观点;④提供的选择答案要尽可能全面;⑤问卷应简洁.
A.①②④⑤ B.①③④⑤
C.①②③④⑤ D.①⑤
 问题情境
问题情境| a |
| x |
| 1 |
| x |
| x | … |
|
|
|
1 | 2 | 3 | 4 | … | ||||||
| y | … | … |
| 1 |
| x |
| 1 |
| x |
| x |
|
| x |
|
| x |
|
| x |
|
| x |
|
| x |
|
| 1 |
| x |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com