阅读下面的短文,并解答下列问题:
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.
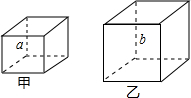
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比(a:b).
设S
甲、S
乙分别表示这两个正方体的表面积,则
=
=(
)
2又设V
甲、V
乙分别表示这两个正方体的体积,则
=
=(
)
3(1)下列几何体中,一定属于相似体的是(A)
A.两个球体B.两个锥体C.两个圆柱体D.两个长方体
(2)请归纳出相似体的三条主要性质:
①相似体的一切对应线段(或弧)长的比等于
;
②相似体表面积的比等于
;
③相似体体积比等于
.
(3)假定在完全正常发育的条件下,不同时期的同一人的人体是相似体,一个小朋友上幼儿园时身高为1.1米,体重为18千克,到了初三时,身高为1.65米,问他的体重是多少?(不考虑不同时期人体平均密度的变化)

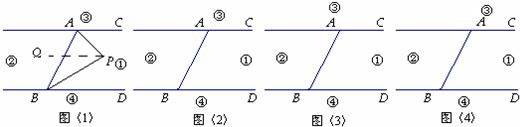
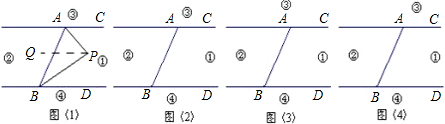
 阅读下面的短文,并解答下列问题:
阅读下面的短文,并解答下列问题: