
题目列表(包括答案和解析)
|
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
阅读材料,解答问题
材料:利用解二元一次方程组的代入消元法可解形如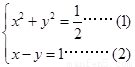 的方程组.
的方程组.
如:由(2)得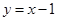 ,代入(1)消元得到关于
,代入(1)消元得到关于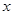 的方程:
的方程:
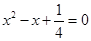 ,
,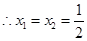
将 代入
代入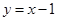 得:
得: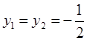 ,
,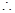 方程组的解为
方程组的解为
请你用代入消元法解方程组:
阅读材料,解答问题
材料:利用解二元一次方程组的代入消元法可解形如 的方程组.
的方程组.
如:由(2)得 ,代入(1)消元得到关于
,代入(1)消元得到关于 的方程:
的方程: ,
,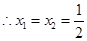
将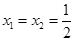 代入
代入 得:
得: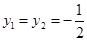 ,
, 方程组的解为
方程组的解为
请你用代入消元法解方程组:
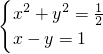 的方程组.
的方程组. =0,∴x1=x2=
=0,∴x1=x2=
 代入y=x-1得y1=y2=-
代入y=x-1得y1=y2=- ,∴方程组的解为
,∴方程组的解为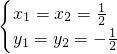 .
.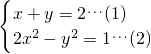 .
.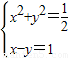 的方程组.
的方程组. =0,∴x1=x2=
=0,∴x1=x2=
 代入y=x-1得y1=y2=-
代入y=x-1得y1=y2=- ,∴方程组的解为
,∴方程组的解为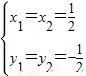 .
.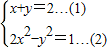 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com