
题目列表(包括答案和解析)
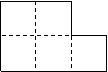
如图,有一块由5个1m×1m的小正方形组成的钢板原料.电焊工王师傅准备将其分割后焊接成一个无重叠无缝隙的正方形形状的工件(不计加工中的损耗).
⑴ 焊接后的正方形工件的边长是 m;
⑵ 请你给出一种分割方法,并在图1中标出裁剪线;
⑶ 根据你的分割方法,在图2中画出拼接后正方形工件的示意图,标出需要焊接的痕迹,并计算焊接线的长度.



![]()
![]()
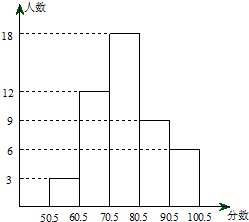 整数).请根据所给信息解答下列问题:
整数).请根据所给信息解答下列问题: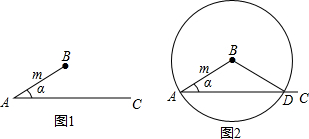

 下面是小明作业中对一道题的解答以及老师的批阅
下面是小明作业中对一道题的解答以及老师的批阅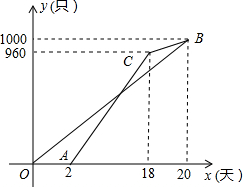 图中线段OB和折线ACB分别表示两车间的加工情况.依据图中提供的信息,完成下列各题:
图中线段OB和折线ACB分别表示两车间的加工情况.依据图中提供的信息,完成下列各题:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com