练习册

  • 练习册
  • 试题
    活 动 内 容 师生互动思考与安排 例1:下列关系式中的y是x的反比例函数吗?如果是.比例系数k是多少? y＝- ,y＝+2,(7)y＝. ［说明］这个例题作了一些变动.引导学生充分讨论.把函数关系式如何化成y＝或y＝kx+b的形式了解函数关系式的变形.知道函数关系式中比例系数的值连同前面的符号.会与一次函数的关系式进行比较.若对反比例函数的定义理解不深刻.常会认为也是反比例函数.而(2)式等号右边的分母是x-1.不是x.(2)式y与x-1成反比例.它不是y与x的反比例函数. 对于(4).等号右边不能化成 的形式.它只能转化为的形式.此时分子已不是常数.所以(4)不是反比例函数. 而(7)中右边分母为2x.看上去和(2)类似.但它可以化成.即k＝-.所以(7)是反比例函数. 通过这个例题使学生进一步认识反比例函数概念的本质.提高辨别的能力. 例2:在函数y＝-1.y＝.y＝x-1.y＝中.y是x的反比例函数的有 个. ［说明］这个例题也是引导学生从反比例函数概念入手.着重从形式上进行比较.识别一些反比例函数的变式,如y＝kx-1的形式. 还有y＝-1通分为y＝.y.x都是变量.分子不是常量.故不是反比例函数.但变为y+1＝可说成(y+1)与x成反比例. 例3:若y与x成反比例.且x＝-3时.y＝7.则y与x的函数关系式为 . ［说明］这个例题引导学生观察.讨论.并回顾以前求一次函数关系式时所用的方法.初步感知用“待定系数法 来求比例系数.并引导学生归纳求反比例函数关系式的一般方法.即只需已知一组对应值即可求比例系数. 【查看更多】

     

    题目列表(包括答案和解析)

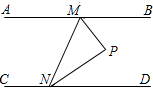    （2013•晋江市质检）如图，动点M、N分别在直线AB与CD上，且AB∥CD，∠BMN与∠MND的角平分线相交于点P，若以MN为直径作⊙O，则点P与⊙O的位置关系是（　　）

    查看答案和解析>>

    如图，动点M、N分别在直线AB与CD上，且AB∥CD，∠BMN与∠MND的角平分线相交于点P，若以MN为直径作⊙O，则点P与⊙0的位置关系是 (?????????? ) .

    A. 点P在⊙O外??????????? B. 点P在⊙O内

    C. 点P在⊙0上　????????? D. 以上都有可能

     

    查看答案和解析>>

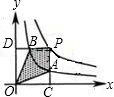    精英家教网两个反比例函数y=
    k
    x
    和y=
    1
    x
    在第一象限内的图象如图所示，点P在y=
    k
    x
    的图象上，PC⊥x轴于点C，交y=
    1
    x
    的图象于点A，PD⊥y轴于点D，交y=
    1
    x
    的图象于点B，当点P在y=
    k
    x
    的图象上运动时，以下结论不正确的是（　　）
    A、△ODB与△OCA的面积相等
    B、四边形PAOB的面积不会发生变化
    C、PA与PB始终相等
    D、当点A是PC的中点时，点B一定是PD的中点

    查看答案和解析>>

    已知电灯电路两端的电压U、灯泡内钨丝的电阻R与通过的电流I的关系式是U=IR．当U为定值时，下面说法正确的是（　　）
    A、I与R成正比例B、I与R成反比例C、U与R成反比例D、U与R成正比例

    查看答案和解析>>

    11、某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程（工作前洗衣机内无水），在这三个过程中洗衣机内水量y（升）与时间x（分）之间的函数关系对应的图象大致为（　　）

    查看答案和解析>>


    同步练习册答案