
题目列表(包括答案和解析)
 (2013•燕山区一模)如图,直线y=2x-1与反比例函数y=
(2013•燕山区一模)如图,直线y=2x-1与反比例函数y=| k | x |
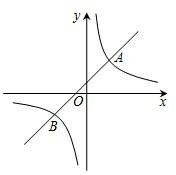 (2013•门头沟区一模)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=
(2013•门头沟区一模)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=| m | x |
 如图所示,一个反比例函数的图象在第二象限内,点A是图象上的任意一点,AM⊥x轴于M,O是原点,若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.
如图所示,一个反比例函数的图象在第二象限内,点A是图象上的任意一点,AM⊥x轴于M,O是原点,若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围. 如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A,B,四边形ABCD是正方形,反比例函数y=
如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A,B,四边形ABCD是正方形,反比例函数y=| k | x |
 到喷药结束的10分钟内(包括第十分钟),y是x的二次函数;喷药结束后(从第十分钟开始),y是x的反比例函数.
到喷药结束的10分钟内(包括第十分钟),y是x的二次函数;喷药结束后(从第十分钟开始),y是x的反比例函数.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com