练习册

  • 练习册
  • 试题
    (一)提出问题,引发讨论 在学习不等式组之前,我们来开展小组活动吧,每个小组的同学准备五根小木棒,使它们的长度依次为3cm.10cm.6cm.9cm和14cm,用这些小木棒来搭三角形,要求所搭成的三角形的三边中必须有3cm和10cm这两根木棒,请大家先想想我们还有多少种不同的搭配方式,它们都能搭出三角形吗?再动手试试,验证你们的想法. 搭配方式有三种:3cm.10cm.6cm;3cm.10cm.9cm;3cm.10cm.14cm.但并不是每种搭配方式都能搭成三角形.要构成三角形,必须有两条较短的边拼起来后要略比长边长,也即“任意两边之和大于第三边 .将此不等式变形后成为“任意两边之差小于第三边 .这样可发现只有一种搭配方式可构成三角形.通过拼图验证可得到如课本P143中图. 用不等式来解释,设第三边长为xcm,则有x>10-3又x<10+3,即x>7与x<13,这二者并不矛盾,比7大比13小的数在数轴上可表示为如图9.3-1-1的阴影部分,在这部分数中任取一个都能与10cm和3cm构成一个三角形,所给的三条边6cm.9cm.14cm中只有9cm符合要求.这就是说第三边的取值必须同时满足两个条件:比7大且比13小,把x>7与x<13组合成一个整体即构成一元一次不等式组,即把两个不等式合起来,组成一个一元一次不等式组.由此例可知不等式组的解集即为各个不等式的解集的公共部分. 【查看更多】

     

    题目列表(包括答案和解析)

    （2012•浦口区一模）提出问题：
    如图，在△ABC中，∠A=90°，分别以边AB、AC向外作正方形ABDE和正方形ACFG，连接EG，小亮发现△ABC与△AEG面积相等．小亮思考：这个问题中，如果∠A≠90°，那么△ABC与△AEG面积是否仍然相等？
    猜想结论：
    经过研究，小亮认为：上述问题中，对于任意△ABC，分别以边AB、AC向外作正方形ABDE 和正方形 ACFG，连接EG，那么△ABC与△AEG面积相等．
    证明猜想：
    （1）请你帮助小亮画出图形，并完成证明过程．已知：以△ABC的两边AB、AC为边长分别向外作正方形ABDE、ACFG，连接GE．求证：S△AEG=S△ABC．
    结论应用：
    （2）学校教学楼前的一个六边形花圃被分成七个部分，分别种上不同品种的花卉，其中四边形ABCD、CIHG、GFED均为正方形，且面积分别为9m2、5m2和4m2．求这个六边形花圃ABIHFE的面积．

    查看答案和解析>>

    提出问题：如图，在“儿童节”前夕，小明和小华分别获得一块分布均匀且形状为等腰梯形和直角梯形的蛋糕（AD∥BC），在蛋糕的边缘均匀分布着巧克力，小明和小华决定只切一刀将自己的这块蛋糕平分（要求分得的蛋糕和巧克力质量都一样）．
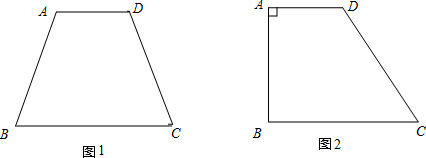
    精英家教网
    背景介绍：这条分割直线既平分了梯形的面积，又平分了梯形的周长，我们称这条线为梯形的“等分积周线”．
    尝试解决：（1）小明很快就想到了一条分割直线，而且用尺规作图作出．请你帮小明在图1中作出这条“等分积周线”，从而平分蛋糕．
    （2）小华觉得小明的方法很好，所以模仿着在自己的蛋糕（图2）中画了一条直线EF分别交AD、BC于点E、F．你觉得小华会成功吗？如能成功，说出确定的方法；如不能成功，请说明理由．
    （3）通过上面的实践，你一定有了更深刻的认识．若图2中AD∥BC，∠A=90°，AD＜BC，AB=4cm，BC=6cm，CD=5cm．请你找出梯形ABCD的所有“等分积周线”，并简要的说明确定的方法．

    查看答案和解析>>

    提出问题：如图，在“儿童节”前夕，小明和小华分别获得一块分布均匀且形状为等腰梯形和直角梯形的蛋糕（AD∥BC），在蛋糕的边缘均匀分布着巧克力，小明和小华决定只切一刀将自己的这块蛋糕平分（要求分得的蛋糕和巧克力质量都一样）．

    背景介绍：这条分割直线既平分了梯形的面积，又平分了梯形的周长，我们称这条线为梯形的“等分积周线”．

    1.小明很快就想到了一条分割直线，而且用尺规作图作出.请你帮小明在图1中作出这条“等分积周线”，从而平分蛋糕．

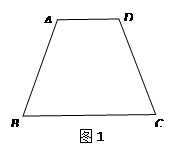
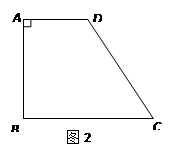
    2.小华觉得小明的方法很好，所以模仿着在自己的蛋糕（图2）中画了一条直线EF分别交AD、BC于点E、F．你觉得小华会成功吗？如能成功，说出确定的方法；如不能成功，请说明理由

    3.通过上面的实践，你一定有了更深刻的认识．若图2中AD∥BC，∠A=90°，AD<BC，AB=4 cm，BC =6 cm，CD= 5cm.请你找出梯形ABCD的所有“等分积周线”，并简要的说明确定的方法．

     

    查看答案和解析>>

    提出问题：如图，在“儿童节”前夕，小明和小华分别获得一块分布均匀且形状为等腰梯形和直角梯形的蛋糕（AD∥BC），在蛋糕的边缘均匀分布着巧克力，小明和小华决定只切一刀将自己的这块蛋糕平分（要求分得的蛋糕和巧克力质量都一样）．
    背景介绍：这条分割直线既平分了梯形的面积，又平分了梯形的周长，我们称这条线为梯形的“等分积周线”．
    【小题1】小明很快就想到了一条分割直线，而且用尺规作图作出.请你帮小明在图1中作出这条“等分积周线”，从而平分蛋糕．


    【小题2】小华觉得小明的方法很好，所以模仿着在自己的蛋糕（图2）中画了一条直线EF分别交AD、BC于点E、F．你觉得小华会成功吗？如能成功，说出确定的方法；如不能成功，请说明理由
    【小题3】通过上面的实践，你一定有了更深刻的认识．若图2中AD∥BC，∠A=90°，AD<BC，AB="4" cm，BC ="6" cm，CD= 5cm.请你找出梯形ABCD的所有“等分积周线”，并简要的说明确定的方法．

    查看答案和解析>>

    提出问题：如图，在“儿童节”前夕，小明和小华分别获得一块分布均匀且形状为等腰梯形和直角梯形的蛋糕（AD∥BC），在蛋糕的边缘均匀分布着巧克力，小明和小华决定只切一刀将自己的这块蛋糕平分（要求分得的蛋糕和巧克力质量都一样）．

    背景介绍：这条分割直线既平分了梯形的面积，又平分了梯形的周长，我们称这条线为梯形的“等分积周线”．

    1.小明很快就想到了一条分割直线，而且用尺规作图作出.请你帮小明在图1中作出这条“等分积周线”，从而平分蛋糕．

    2.小华觉得小明的方法很好，所以模仿着在自己的蛋糕（图2）中画了一条直线EF分别交AD、BC于点E、F．你觉得小华会成功吗？如能成功，说出确定的方法；如不能成功，请说明理由

    3.通过上面的实践，你一定有了更深刻的认识．若图2中AD∥BC，∠A=90°，AD<BC，AB=4 cm，BC =6 cm，CD= 5cm.请你找出梯形ABCD的所有“等分积周线”，并简要的说明确定的方法．

     

    查看答案和解析>>


    同步练习册答案