
题目列表(包括答案和解析)
我们在用玩具枪瞄准时,总是用一只眼对准准星和目标,用数学知识解释为__________________ .
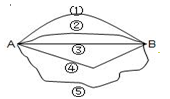
图,已知从A地到B地共有三条路,小红应选择第 路最近,用数学知识解释为 .
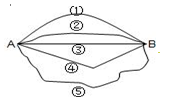
 如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,这种做法用几何知识解释应是( )
如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,这种做法用几何知识解释应是( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com