(以下两小题选做一题,第1小题满分14分,第2小题满分为10分.若两小题都做,以第1小题计分)
选做第
小题.
(1)一张矩形纸片OABC平放在平面直角坐标系内,O为原点,点A在x的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
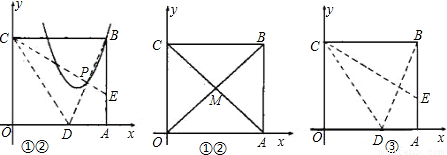
①如图,将纸片沿CE对折,点B落在x轴上的点D处,求点D的坐标;
②在①中,设BD与CE的交点为P,若点P,B在抛物线y=x
2+bx+c上,求b,c的值;
③若将纸片沿直线l对折,点B落在坐标轴上的点F处,l与BF的交点为Q,若点Q在②的抛物线上,求l的解析式.
(2)一张矩形纸片OABC平放在平面直角坐标系内,O为原点,点A在x的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
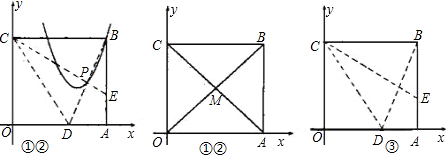
①求直线AC的解析式;
②若M为AC与BO的交点,点M在抛物线y=-
x
2+kx上,求k的值;
③将纸片沿CE对折,点B落在x轴上的点D处,试判断点D是否在②的抛物线上,并说明理由.




 的最小值是______;
的最小值是______;
 x2+kx上,求k的值;
x2+kx上,求k的值;