
题目列表(包括答案和解析)


| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 4 |
| 9 |
| 1 |
| 4 |
| 4 |
| 9 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20122 |
| 1 |
| 20132 |
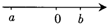 实数a、b在实数轴上对应点的位置如图所示,则
实数a、b在实数轴上对应点的位置如图所示,则| a2-2ab+b2 |
| A、a-b | B、b-a |
| C、a+b | D、-a-b |

| 1 |
| 3 |
| 2 |
| 3 |
下列说法正确的是( )
| A.多项式a2﹣2ab﹣b2可以分解成(a﹣b)2 |
| B.(a﹣b)2与a2﹣b2相等 |
| C.x2+2x+1不能运用完全平方公式因式分解 |
| D.多项式8x3+24x2y+18xy2可分解为2x(2x+3y)2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com