
题目列表(包括答案和解析)
猜想规律型问题是目前中考的一大热点,原因在于猜想本身就是重要的数学方法,更是人们探索发现知识的重要手段.此类题不但能培养学生分析、归纳、解决问题的能力,也非常有利于学生创造性思维的培养.对于有关图形的规律探索问题,更能考查学生的观察读图能力.笔者认为做此类题不妨在用眼观察的同时也用笔做一有序列举,
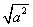 的值为________;当a=2时,计算
的值为________;当a=2时,计算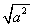 的值为________;
的值为________; 时, 计算
时, 计算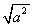 的值为________;当a=0时,计算
的值为________;当a=0时,计算 的值为________;
的值为________; 的值为________;当a=-2时,计算
的值为________;当a=-2时,计算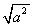 的值为________;
的值为________;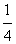 时,计算
时,计算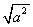 的值为_________。
的值为_________。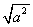 的值,这样对于任意数a,
的值,这样对于任意数a, 一定等于a吗?你能发现什么结论吗?
一定等于a吗?你能发现什么结论吗? 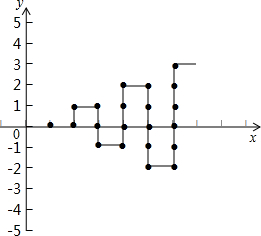
 如图,在平面直角坐标系中,有若干个整数点,按顺序(0,0),(1,0),(1,1),(2,1),(2,0),(2,-1)…这样排列.根据这个规律探索可知,第10个点的坐标为
如图,在平面直角坐标系中,有若干个整数点,按顺序(0,0),(1,0),(1,1),(2,1),(2,0),(2,-1)…这样排列.根据这个规律探索可知,第10个点的坐标为| 编号 | 教学方式 | 最喜欢的频数 | 频率 |
| 1 | 教师讲,学生听 | 20 | 0.10 |
| 2 | 教师提出问题,学生探索思考 | ||
| 3 | 学生自行阅读教材,独立思考 | 30 | |
| 4 | 分组讨论,解决问题 | 0.25 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com